Полярна система координат.
Крім афінної системи координат і її часткового випадку - прямокутної системи координат, часто розглядають і застосовують полярну систему координат на площині. Її використовують тому, що в науці і техніці зустрічаються криві, які простіше описати і побудувати саме в такій системі координат. Візьмемо на орієнтованій площині точку О і одиничний вектор Означення 7. Геометричний образ, який складається з точки О і вектора Означення 8. Елементами полярної системи координат є точка О, яка називається полюсом, і промінь ОХ, який називається полярною віссю, яка проходить через точку О і паралельна вектору Означення 9. Положення точки М на площині визначається відстанню від цієї точки до полюса – полярним радіусом
(рис. 3)
Дві координати (
Зв’язок між полярними і прямокутними декартовими координатами точки на площині. Якщо початок декартової прямокутної системи координат сумістити з полюсом, а вісь ОХ направити по полярній осі (рис. 4), то прямокутні координати х, у точки М та її полярні координати
(рис. 4) По заданим х, у кут
Відстань між двома точками A (ρ1;φ1) і в B (ρ2; φ2) (рис. 5), заданими полярними координатами, обчислюється за формулою:
φ2-φ1 A (ρ1; φ1) ρ1 О (рис. 5) Площа трикутника ОАВ в полярній системі координат обчислюється за формулою:
Полярно-циліндрова система координат При рішенні різних задач іноді доводиться розглядати в просторі і так звану полярно-циліндрову систему координат. точки М;
x = r cos φ; y = r sin φ; z = z. (1)
Таким чином, якщо задані полярно-циліндрові координати r,
|

 .
. і кутом між радіусом і полярною віссю – полярним кутом
і кутом між радіусом і полярною віссю – полярним кутом  . Ці два числа
. Ці два числа 

 , при цьому кут
, при цьому кут 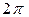 , а також від’ємні кути, тобто кути, які відраховуються від полярної осі за напрямком руху годинникової стрілки.
, а також від’ємні кути, тобто кути, які відраховуються від полярної осі за напрямком руху годинникової стрілки.

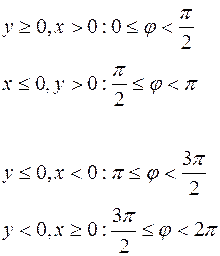

 В (ρ2; φ2)
В (ρ2; φ2)

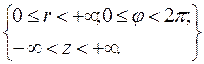
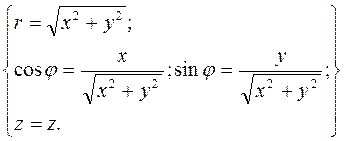 (2)
(2)


