Полярно-сферична система координат
Іноді доводиться розглядати в просторі і так звану полярно-сферичну систему координат. В полярно-сферичній системі координат точка М задається трьома впорядкованими числами: 1) відстанню, яка називається полярно-сферичним радіусом точки М; Ця впорядкована трійка чисел називається полярно-сферичними або просто сферичними координатами точки.
x = r cosφ cos θ; y = r sin φ cos θ; z = r sin θ (1)
Таким чином, якщо задані полярно-сферичні координати r, Питання для самоперевірки. 1. Що називається афінною системою координат на площині? У чому відмінність афінної системи координат від прямокутної декартової? 2. Що називається радіусом-вектором точки? Чи зміняться радіус-вектори точок, якщо: а) змінити напрямок координатних осей, залишивши початок без зміни; б) змінити початок координат, залишивши напрямок осей без зміни? 3. Чи можуть дві різні точки в одній системі координат мати рівні радіус-вектори? 4. Що називається координатами точки в системі координат? 5. Якщо М ділить відрізок АВ у відношенні λ, то в якому відношенні ділить М відрізок ВА? 6. Як обчислюють координати точки М, яка ділить відрізок АВ? 7. Як обчислюється відстань між двома точками в прямокутній декартовій системі координат? 8. Як обчислюється площа трикутника в прямокутній декартовій системі координат? 9. Що називається полярною системою координат? Які вона має основні елементи? Як зміняться полярні координати точки М (ρ;; φ;), якщо залишити без зміни полюс О, полярну вісь Ох, але змінити на зворотній додатній напрямок обходу? 10. Який зв'язок між полярними і прямокутними декартовими координатами точки на площині? (формули). 11. Як обчислюється відстань між двома точками і площа трикутника в полярній системі координат? 12. Як розташовані точки на площині, полярні координати яких задовольняють одній з наступних умов: а) ρ; = 3; б) φ; = Методичні вказівки до розв’язування задач.
1. На осях координат знайти точки, кожна з яких рівновіддалена від точок А (1;1) і В (3;7). Розв’язання: Нехай М1 і М2 – точки, які потрібно знайти, і точка М1 лежить на осі Ох, тоді її координати (х;0); точка М2 лежить на осі Оу, тоді її координати (0; у). Так як точки М1 і М2 однаково віддалені від точок А і В, то ρ; (М1,А)= ρ; (М1,В) і ρ; (М2,А)= ρ; (М2,В). За формулою
Розв’язуючи отримані рівняння, знайдемо х =14 і у = Тоді М1 (14;0) і М2 Відповідь: М1 (14;0) і М2
2. Визначити площу паралелограма, три вершини якого лежать в точках А (-2; 3), В (4; -5) і С (-3; 1). Розв’язання: Площа Ѕ паралелограма, яку потрібно знайти, дорівнює подвоєній площі трикутника АВС, тобто Ѕ = 2 ЅΔАВС. Тоді, за формулою, ЅΔАВС =
Відповідь: Ѕ =20.
3. Три послідовні вершини паралелограма мають координати А (3; -3), В (-1; 1) і С (1; 6). Знайти координати четвертої вершини D. Розв’язання: Знаючи те, що діагоналі паралелограма в точці Е перетину діляться навпіл, знайдемо цю точку як середину відрізка АС. Якщо її координати позначити через х1 і у1, то за формулами
А якщо через х2 і у2 – координати точки D, то за формулами звідки х2 = 5, у2 = 2, D (5; 2). Відповідь: D (5; 2).
4. Вершини трикутника знаходяться в точках А (3; -5), В (-3; 3) і С (-1; -2). Знайти довжину бісектриси його внутрішнього кута при вершині А. Розв’язання: Відомо, що бісектриса внутрішнього кута трикутника ділить протилежну сторону на частини, пропорційні довжинам прилеглих сторін. Знайдемо довжини цих сторін:
Тоді якщо D (х; у) – точка перетину бісектриси і сторони ВС (рис. 6), то вона ділить цю сторону у відношенні
Тепер знайдемо координати точки D:
Знайдемо довжину бісектриси:
Відповідь:
С (-1; -2)
А (3; -5) В (-3; 3) рис. 6
5. В точках М1 (х1; у1); М2 (х2; у2) і М3 (х3; у3) зосереджені маси m1, m2, m3. Знайти центр ваги цієї системи. Розв’язання: Знайдемо спочатку центр ваги М' (х'; у') системи двох мас m1 і m2, зосереджених в точках М1 і М2. З механіки відомо, що центр ваги цих мас ділить відрізок М1М2 на частини, обернено пропорційні масам, зосередженим на кінцях відрізка, тобто у відношенні λ'= За формулою точки М:
Якщо точка М (х; у) – центр ваги системи трьох мас m1, m2, m3, то вона ділить відрізок М' М3 на частини пропорційні масам, зосередженим в точках М' і М3, тобто у відношенні λ=
6. Знайти радіус вписаного в трикутник кола, якщо одна його вершина лежить в полюсі полярної системи координат, а інші в точках А (2; 0), В (4; Розв’язання: З геометрії відомо, що Площу трикутника обчислимо за формулою
Довжини двох сторін трикутника, а саме ОА і ОВ, відомі, вони рівні відповідно 2 і 4 (рис. 7). Довжину сторони АВ знайдемо за формулою: АВ = Тоді
Відповідь:
О А(2;0) Р рис. 7 7. В полярній системі координат дано точки А (3; Розв’язання: Нова система координат отримана зі старої поворотом полярної осі на кут, величина якого дорівнює α= Тоді нові координати ρ' і θ' точки В будуть наступними: ρ' =1, θ'= Відповідь: 8. Знайти полярні координати точки А, якщо її координати х = -1, у = Розв’язання: За відомими формулами маємо:
Так як точка А лежить в другій координатній чверті (х <0, у >0), то θ;= Відповідь: А 9. Знаючи полярні координати точки А Розв’язання: Введемо допоміжну прямокутну декартову систему координат О'Χ'Υ', початок О' і вісь О'Χ' співпадає з полярною віссю (рис. 8). Тоді координати точки А в полярній системі і в системі О'Χ'Υ' зв’язані співвідношеннями х = ρ соs θ;, y = ρ sin θ;. Звідки Тоді остаточно маємо: Відповідь:
О 2 х
рис. 8
Завдання для самостійної роботи Варіант 0 1. Вершини заданого трикутника АВС знаходяться в точках А (3; -5), В (-3; 3) і С (-1; -2). Знайти довжину бісектриси його внутрішнього кута при вершині А. Розв’язок: Відомо, що бісектриса кута трикутника ділить протилежну сторону на відрізки, пропорційні довжинам прилеглих сторін. Тобто: Знайдемо довжини сторін АВ і АС:
Отже, точка D (х; у) ділить сторону ВС у відношенні:
Знайдемо координати точки D за формулами:
Тоді D Тепер довжина бісектриси АD дорівнює:
Відповідь: AD = 2. Знайти центр мас однорідного стержня з кінцями в точках А (5; -4) і В (7; 8). Розв’язок: Так як центр мас однорідного стержня розташовані в його середині, то потрібно знайти середину відрізка АВ. х = Центр мас однорідного стержня АВ знаходиться в точці С (6; 2). Відповідь: С (6; 2). 3. Визначити площу трикутника, три вершини якого мають координати А (-2; 3), В (4; -5) і С (-3; 1). Розв’язок: Площа Ѕ трикутника обчислюється за формулою
Тоді маємо:
Відповідь: Ѕ = 10. 4. В полярній системі координат дано точки А (3; Розв’язок: Нова система координат отримана зі старої поворотом полярної осі на кут, величина якого дорівнює α= Тоді нові координати ρ' і θ' точки В будуть наступними: ρ' = 1, θ' = Відповідь: 5. Одна з вершин трикутника ОАВ знаходиться в полюсі О, дві інші А Розв’язок: Площа трикутника в полярній системі координат обчислюється за формулою:
Відповідь: S = 1.
Варіант 1 1. Знайти відношення, в якому площина ХОУ ділить відрізок АВ, якщо А (3; -6; -1) і В (9; 7; 5). 2. Вершини заданого трикутника АВС знаходяться в точках А (4; 1), В (7; 5) і С (-4; 7). Знайти довжину бісектриси його внутрішнього кута при вершині А. 3. Визначити площу трикутника, вершини якого мають координати А (4; 2), В (9; 4), С (7; 6). 4. Визначити полярні координати точок, симетричних відносно полярної вісі точкам М1 М5 (5; -1), які задані в полярній системі координат. 5. В полярній системі координат дано дві суміжні вершини квадрату М1 Варіант 2 1. Знайти координати точки, яка рівновіддалена від трьох даних точок (2; 2), (5; 1), (7; -3). 2. Задані координати кінців А (-1; 5), В (3; 4) однорідного стержня. Визначити координати його центру тяжіння. 3. Визначити площу п’ятикутника, вершинами якого є точки А (-2; 0), В (0; -1), С (2; 0), D (3; 2), E (-1; 3). 4. Визначити полярні координати точок симетричних відносно полюса точкам М1 М5 (3; -2), які задані в полярній системі координат. 5. В полярній системі координат дано дві протилежні вершини квадрату P Варіант 3 1. Знайти координати точки, яка рівновіддалена від трьох даних точок (5; 4), (3; 8), (-2; -7). 2. Дано координати точок Р (-1; 5), Q (3; 2). Знайти координати точки М, симетричній точці Р щодо точки Q. 3. Визначити площу трикутника АВС з вершинами А (2; 1), В (3; 4), С (1; 6). 4. В полярній системі координат дано дві вершини А В 5. В полярній системі координат дано дві вершини правильного трикутника А Варіант 4 1. Знайти координати точки, яка рівновіддалена від трьох даних точок (2; 3), (4; -1), (5; 2). 2. Дано координати точок Р (-1; 5), Q (3; 2). Знайти координати точки N, симетричній точці Q щодо точки Р. 3. Визначити площу трикутника АВС з вершинами А (-2; 4), В (0; -3), С (1; 7). 4. В полярній системі координат дано точки А 5. Одна з вершин трикутника ОАВ знаходиться в полюсі, дві інші А Варіант 5 1. Визначити радіус кола, яке проходить через точку (-2; 1) і має центр в точці (2; -3). 2. Дано дві суміжні вершини паралелограма А (-4; 4), В (2; 8) і точка перетину М (2; 2) його діагоналей. Визначити дві інші вершини C і D. 3. Визначити площу трикутника АВС з вершинами А (5; 4), В (11; 0), С (0; 3). 4. В полярній системі координат дано точки А С 5. Одна з вершин трикутника ОАВ знаходиться в полюсі О, дві інші А Варіант 6 1. Дано координати вершин трикутника АВС: А (4; 1), В (7; 5), С (-4; 7). Знайти довжину бісектриси AD кута А. 2. Дано чотирикутник А (-1; 7), В (5; 5), C (7; -5), D (3; -7). Довести, що відрізки, які сполучають середини сторін АD і ВС, АВ і СD, перетинаються і діляться точкою перетину навпіл. 3. Визначити відстань від точки (2; 0) до прямої, яка проходить через точки (1; 1) і (5; 4). 4. У полярній системі координат дано точки М1 5. Обчислити площу трикутника, вершини якого А В Варіант 7 1. Визначити довжину медіани АМ трикутника АВС, заданого координатами своїх вершин: А (5; -4), В (-1; 2), С (5; 1). 2. Показати, що чотирикутник, вершинами якого служать середини сторін даного чотирикутника, є паралелограм. 3. Визначити відстань від початку координат до прямої, яка проходить через точки (1; 5) і (5; 4). 4. В полярній системі координат дано точки М1 М2 5. Полюс полярної системи координат співпадає з початком декартових прямокутних координат, а полярна вісь співпадає з додатною піввіссю абсцис. В полярній системі координат дано точки М1 Варіант 8 1. Довести, що трикутник АВС з координатами А (1; 1), В (2; 5), С (-6; 7) є прямокутним. Вказати вершину прямого кута. 2. Дано дві протилежні вершини квадрата А (-1; 4) і С (7; -2). Знайти дві інші вершини. Система координат прямокутна декартова. 3. Дві вершини трикутника знаходяться в точках (5; 1) і (-2; 2), третя вершина – на вісі Ох. Знаючи, що площа трикутника дорівнює 10, знайти третю вершину. 4. В полярній системі координат дано точки М1 5. Полюс полярної системи координат співпадає з початком декартових прямокутних координат, а полярна вісь співпадає з додатною піввіссю абсцис. В декартовій прямокутній системі координат дано точки М1 (0; 5), М2 (-3; 0), М3 Варіант 9 1. Знайти координати центра і радіуса кола, яке проходить через точку В (-10; 4) і дотикається до вісі Ох в точці А (-6; 0). 2. Визначати координати точок, що ділять відрізок А (2; 3), В (-1; 2) у відношенні 3. Площа трикутника S = 3, дві його вершини А (3; 1) і В (1; -3), центр ваги цього трикутника лежить на вісі Ох. Визначити координати третьої вершини С. 4. В полярній системі координат дано точки М1 5. Нехай Оij – дана прямокутна декартова система, а Оі – полярна система, при цьому додатній напрямок обходу вибраний так, що М1 (0; 6), М2 (-2; 0), М3 (-1; 1), М4 Варіант 10 1. Знайти координати центра і радіус кола, яке проходить через точку А (-8; 4) і дотикається вісей координат. 2. Дві вершини трикутника АВС мають координати А (3; 6), В (-3; 5). Визначити координати вершини при умові, що середини сторін АС і ВС лежать на різних вісях координат. 3. Обчислити площу трикутника, вершини якого точки А (2; -3), В (3; 2), С (-2; 5). 4. Дано правильний трикутник АВС, сторона якого дорівнює 5. Прийняв вершину А за полюс полярної системи координат, а направлену пряму АВ за полярну вісь, визначити полярні координат вершин і центр Р трикутника. Розглянути два можливих випадки розташування трикутника відносно полярної вісі. 5. Обчислити площа трикутника, одна з вершин якого знаходиться в полюсі, а дві інші мають полярні координати А1 А2 Варіант 11 1. На вісях координат знайти точки, кожна з яких рівновіддалена від точок (1; 1) і (3; 7). 2. На прямій m узяті послідовно точки А1, А2, А3, А4, А5, А6 так, що А1А2 = А2А3 = А3А4 = А4А5 = А5А6. Знаючи координати точок А2 (2; 5) і А5 (-1; 7) в загальній декартовій системі координат, визначити відношення, в яких точки А1, А3, А4, та А6 ділять відрізок А2А5, а також координати цих точок. 3. Обчислити площу трикутника, вершини якого точки А (-3; 2), В (5; -2), С (1; 3). 4. Обчислити відстань між двома точками А 5. Трикутник АВС заданий полярними координатами вершин А Варіант 12 1. Вершини чотирикутника знаходяться в точках А (1; -3), В (8; 0), С (4; 8), D (-3; 5). Показати, що АВСD є паралелограм. 2. Знаючи координати вершин А (3; -1), В (6; 7), С (-9; 3) трикутника АВС, обчислити координати точки перетину його медіан. 3. Обчислити площу трикутника, вершини якого точки А (3; -4), В (-2; 3), С (4; 5). 4. Дано квадрат ABCD, сторона якого дорівнює 3. Прийняв вершину А за полюс полярної системи координат, а направлену пряму АВ за полярну вісь, визначити координати його вершин і точки Р перетину діагоналей. Розглянути два можливих випадки розташування квадрата відносно полярної вісі. 5. Обчислити площу трикутника, одна з вершин якого знаходиться в полюсі, а дві інші мають полярні координати А1 Варіант 13 1. Вершини чотирикутника знаходяться в точках А (1; 1), В (2; 3), С (5; 0), D (7; -5). Показати, що АВСD є трапеція. 2. Дано вершини А (2; -3; -5), В (-1; 3; 2) і точку Е (4; -1; 7) перетину діагоналей паралелограма АВСD. Знайти дві інші вершини цього паралелограма. 3. Дано вершини трикутника А (3; 6), В (-1; 3), С (2; -1). Обчислити довжину його висоти, яка проведена з вершини С. 4. Дано правильний шестикутник ABCDEF, сторона якого дорівнює а. Прийняв вершину А за полюс полярної системи координат, а направлену пряму АВ за полярну вісь, визначити координати всіх його вершин і точки Р перетину діагоналей. Розглянути два можливих випадки розташування шестикутника відносно полярної вісі. 5. Обчислити площу трикутника, одна з вершин якого знаходиться в полюсі, а дві інші мають полярні координати А1 А2 Варіант 14 1. Дано три вершини паралелограма А (-1; 3), В (2; -5), С (0; 4). Визначити четверту вершину D, протилежну В. 2. Дано вершини М1 (3; 2; -5), М2 (1; -4; 3), М3 (-3; 0; 1) трикутника. Знайти середини його сторін. 3. Дано три вершини паралелограма А (-2; 3), В (4; -5), С (-3; 1). Обчислити його площу. 4. Знайти полярні координати точок, які симетричні з точками М1 5. Вершини трикутника знаходяться в точках А В Варіант 15 1. Дано дві суміжні вершини квадрата А (-2; 1), В (3; 3). Знайти дві інші вершини. 2. Дано три вершини А (3; -4; 7), В (-5; 3; -2), С (1; 2; -3) паралелограма АВСD. Знайти його четверту протилежну В вершину D. 3. Дано три вершини паралелограма А (3; 7), В (2; -3), С (-1; 4). Обчислити довжину його висоти, яка опущеної з вершини В на сторону АС. 4. Знайти полярні координати точок, які симетричні з точками М1
5. Дано полярні координати вершин трикутника А В Варіант 16 1. Дано дві вершини рівностороннього трикутника А (-3; 2), В (1; 4). Знайти третю вершину С. 2. Дано три вершини А (3; -1; 2), В (1; 2; -4), С (-1; 1; 2) паралелограма. Знайти його четверту вершину D. 3. Дано послідовні вершини однорідної чотирикутної пластини А (2; 1), В (5; 3), С (-1; 7), D (-7; 5). Визначити координати її центра ваги. 4. Знайти відстань між точками 5. Обчислити площу трикутника, одна з вершин якого знаходиться в полюсі, а дві інші мають полярні координати Варіант 17 1. Центр О і вершина А правильного шестикутника АВСDЕF мають координати О (-1; 2), А (1; 4). Знайти координати інших вершин. 2. Дано вершини А (1; 2; -1), В (2; -1; 3), С (-4; 7; 5) трикутника. Обчислити довжину його бісектриси, проведеної з вершини В. Система координат прямокутна. 3. Дано послідовні вершини однорідної п’ятикутної пластини А (2; 3), В (0; 6), С (-1; 5), D (0; 1), E (1; 1). Визначити координати її центра ваги. 4. Знайти відстань між точками 5. Нехай Оі – дана полярна система координат, Оij – прямокутна декартова система, при цьому вектор j отриманий з вектора і поворотом на +900. Дано полярні координати точок А
Варіант 18 1. Вершини трикутника А (5; 0), В (0; 1), С (3; 3). Обчислити його внутрішні кути. 2. Визначити координати кінців відрізка прямої, який точками С (2; 0; 2) і D (5; -2; 0) ділиться на три рівні частини. 3. Площа трикутника S = 3, дві його вершини точки А (3; 1), В (1; -3), а третя вершина С лежить на вісі Оу. Обчислити координати вершини С. 4. Знайти відстань між точками 5. В полярній системі координат дано дві суміжні вершини квадрату М1 Варіант 19 1. Знайти відстань від початку координат до точок А (11; 4), В (-3; 4). 2. Дано вершини А (1; -1; -3), В (2; 1; -2), С (-5; 2; -6) трикутника. Обчислити довжину бісектриси його внутрішнього кута, проведеної з вершини А. 3. Площа трикутника S = 4, дві його вершини точки А (2; 1), В (3; -2), а третя вершина С лежить на вісі Ох. Обчислити координати вершини С. 4. Дано полярні координати точок А 5. Обчислити площа трикутника, одна з вершин якого знаходиться в полюсі, а дві інші мають полярні координати А1 А2 Варіант 20 1. Знайти відстань від початку координат до точок А (-11; 0), В (5; 12). 2. Дано вершини А (2; -1; 4), В (3; 2; -6), С (-5; 0; 2) трикутника. Обчислити довжину медіани, проведеної з вершини А. Система координат прямокутна. 3. Площа трикутника S = 3, дві його вершини точки А (3; 1), В (1; -3). Центр ваги цього трикутника лежить на вісі Ох. Обчислити координати вершини С. 4. Відносно полярної системи координат дана точка А 5. Одна з вершин трикутника ОАВ знаходиться в полюсі, дві інші А Варіант 21 1. На вісі Оу знайти точку, рівновіддалену від точки (-8; -4) і від початку координат. 2. Знаючи координати середин А1, В1, С1 сторін трикутника, знайти координати його вершин, якщо: А1 (1; 4), В1 (-1; 0), С1 (3; 2). 3. Площа паралелограма S = 12; дві його вершини точки А (-1; 3) і В (-2; 4). Знайти дві інші вершини цього паралелограму, при умові, що точка перетину його діагоналей лежить на вісі абсцис. 4. Відносно полярної системи координат дана точка А 5. В полярній системі координат дано дві протилежні вершини квадрату P Варіант 22 1. Встановити, чи буде трикутник АВС: А (3; 1), В (7; 5), С (5; -1), гострокутним, прямокутним або тупокутним. 2. Знаючи координати середин А1, В1, С1 сторін трикутника, знайти координати його вершин, якщо: А1 (2; -3), В1 (1; 6), С1 (-1; 2). 3. Площа паралелограма S = 17 кв. од.; дві його вершини точки А (2; 1) і В (5; -3). Знайти дві інші вершини цього паралелограму, при умові, що точка перетину його діагоналей лежить на вісі ординат. 4. Обчислити відстань між двома точками Е 5. Дано полярні координати вершин трикутника А В Варіант 23 1. На вісях координат знайти точки, які віддалені від точки М (-5; 9) на відстані 15. 2. Знаючи координати середин А1, В1, С1 сторін трикутника, знайти координати його вершин, якщо: А1 (1; 2), В1 (4; 1), С1 (3; -1). 3. Обчислити площу неорієнтованого чотирикутника, вершини якого точки А (1; 3), В (-2; 0), С (4; 3), D (-3; 5). 4. Обчислити відстань між двома точками C 5. Знаючи прямокутні координати точок А (-1; 1), В (0; 2), С (5; 0), знайти їх полярні координати. Варіант 24 1. Дано коло з центром в точці С (6; 7) і радіусом r = 5. Із точки А (7; 14) до цього кола проведені дотичні. Знайти їх довжини. 2. Знаючи координати середин А1, В1, С1 сторін трикутника, знайти координати його вершин, якщо: А1 (-3; 4), В1 (2; 3), С1 (-2; 0). 3. Дві вершини орієнтованого трикутника АВС знаходиться в точках А (1; 2) і В (5; -1), а третя вершина С на вісі Ох. Знайти координати вершини С, якщо площа трикутника S = 2. 4. В полярній системі координат дано точки А 5. Знайти полярні координати точки М, знаючи її декартові координати х = 8, у = -6. Варіант 25 1. Із точки С (-4; -6), як із центра радіусом r = 10 описане коло. Знайти точки його перетину з бісектрисами координатних кутів. 2. Знаючи координати середин А1, В1, С1 сторін трикутника, знайти координати його вершин, якщо: А1 (-2; 0), В1 (5; 1), С1 (1; -2). 3. Знайти відстань d від точки А (6; -8) до прямої, яка проходить через точки В (-5; 0) і С (3; 6). 4. Відносно полярної системи координат дано точки А В 5. Знайти прямокутні координати точок, які задані своїми полярними координатами А Відповіді Варіант 1 1. 2. 3. 7 4. 5. Варіант 2 1. (2; -3) 2. 3. 12,5 4. 5. Варіант 3 1. (-4; 2) 2. М (7; -1) 3. 4 4. C 5. Варіант 4 1. (3; 1) 2. N (-5; 8) 4. 5. Варіант 5 1. 2. C (8, 0), D (2, -4) 3. 13 4. A 5. 5 Варіант 6 1. AD = 2. - 3. 4. М1 (3; 0), M2 5. Варіант 7 1. 2. - 4. 5. M1 (0; 6), M2 (5; 0), M3 M6 Варіант 8 1. - 2. B (6; 5), D (0; -3) 4. 5. M1 Варіант 9 1. C (-6; 4), r = 4 2. 3. (5; 2) або (2; 2) 4. d = 7 5. М1 М6 Варіант 10 1. Має два розв’язки C1 (-20; 20) r1 = 20, C2 (-4; 4) r2 = 4 2. Існує дві точки, які задовольняють умові С1 (-3; -5) та С2 (3; -6) 3. 14 4. Перший випадок А (0; 0), В (5; 0), С
|

 , яка називається першим полярно-сферичним кутом;
, яка називається першим полярно-сферичним кутом;  , яка називається другим полярно-сферичним кутом.
, яка називається другим полярно-сферичним кутом.
 (2)
(2) ?
? маємо:
маємо:


 .
. маємо:
маємо:
 маємо:
маємо: 
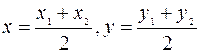 маємо:
маємо:  ,
,






 D
D .
. знайдемо координати
знайдемо координати
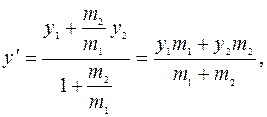
 . Тоді
. Тоді

 , де Ѕ –площа трикутника, р – його півпериметр.
, де Ѕ –площа трикутника, р – його півпериметр.


 і
і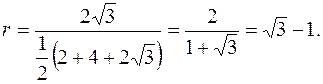

 В (4;
В (4;  )
) ). Полярна вісь повернена так, що у новому положенні вона проходить через точку А. Визначити координати точки В у новій системі координат.
). Полярна вісь повернена так, що у новому положенні вона проходить через точку А. Визначити координати точки В у новій системі координат.

 (полярна вісь співпадає з додатною піввіссю Ох).
(полярна вісь співпадає з додатною піввіссю Ох). ,
,  θ=-
θ=- 

 , знайти її прямокутні декартові координати, якщо полюс О' в декартовій системі координат має координати (2;3), а полярна вісь паралельна осі Ох і співпадає з нею на напрямком.
, знайти її прямокутні декартові координати, якщо полюс О' в декартовій системі координат має координати (2;3), а полярна вісь паралельна осі Ох і співпадає з нею на напрямком. , а її координати в системах ОΧΥ; і О'Χ'Υ' зв’язані співвідношеннями х = х' + а, у = у' + b (перетворення прямокутних декартових координат при паралельному переносі осей).
, а її координати в системах ОΧΥ; і О'Χ'Υ' зв’язані співвідношеннями х = х' + а, у = у' + b (перетворення прямокутних декартових координат при паралельному переносі осей).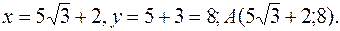

 у у'
у у'
 А
А 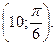


 3 О' х'
3 О' х'

 .
.


 .
.
 .
. .
.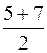 = 6; у =
= 6; у =  = 2
= 2
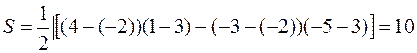
 і В
і В 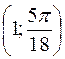 . Визначити площу цього трикутника.
. Визначити площу цього трикутника. Тоді маємо:
Тоді маємо: = 1.
= 1. , М2
, М2  , М3
, М3  , М4 (1; 2),
, М4 (1; 2), і М2
і М2  . Визначити його площу.
. Визначити його площу. , М2
, М2  , М3
, М3  , М4
, М4  ,
, , Q
, Q  . Визначити його площу.
. Визначити його площу. ,
, паралелограму АВСD, точка перетину діагоналей якого співпадає з полюсом. Визначити дві інші вершини цього паралелограму.
паралелограму АВСD, точка перетину діагоналей якого співпадає з полюсом. Визначити дві інші вершини цього паралелограму. , В
, В  . Визначити його площу.
. Визначити його площу.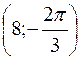 і В
і В  . Визначити полярні координати середини відрізка, який з’єднує точки А і В.
. Визначити полярні координати середини відрізка, який з’єднує точки А і В. і В
і В  . Визначити площу цього трикутника.
. Визначити площу цього трикутника.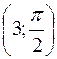 , В
, В  ,
, , D
, D  , E (3; 2), F (2; -1). Додатне положення полярної осі змінено на протилежне. Визначити полярні координати цих точок у новій системі.
, E (3; 2), F (2; -1). Додатне положення полярної осі змінено на протилежне. Визначити полярні координати цих точок у новій системі. і В
і В  . Визначити площу цього трикутника.
. Визначити площу цього трикутника. , М2
, М2  , М3 (2; 0), М4
, М3 (2; 0), М4  , М6
, М6 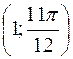 . Полярна вісь повернута так, що у новому положенні вона проходить через точку М1. Визначити координати заданих точок у новій полярній системі.
. Полярна вісь повернута так, що у новому положенні вона проходить через точку М1. Визначити координати заданих точок у новій полярній системі. ,
, , С
, С  задані в полярних координатах.
задані в полярних координатах. ,
, . Обчислити полярні координати середини відрізка, який з’єднує точки М1 і М2.
. Обчислити полярні координати середини відрізка, який з’єднує точки М1 і М2. , М2 (5; 0), М3
, М2 (5; 0), М3  , М4
, М4  , М5
, М5  , М6
, М6  . Визначити декартові координати цих точок.
. Визначити декартові координати цих точок.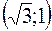 , М4
, М4  , М5
, М5  . Визначити полярні координати цих точок.
. Визначити полярні координати цих точок. ,
, 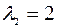 ,
,  ,
,  .
. . Обчислити відстань d між ними.
. Обчислити відстань d між ними. . Визначити полярні координати наступних точок
. Визначити полярні координати наступних точок ,
, .
. і В
і В  .
. , В
, В  , С
, С 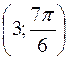 . Довести, що трикутник рівнобедрений.
. Довести, що трикутник рівнобедрений. , А2
, А2  .
. ,
, .
. , М2
, М2  , М4
, М4  відносно полюса.
відносно полюса. ,
, , С
, С  . Довести, що трикутник АВС прямокутний.
. Довести, що трикутник АВС прямокутний. ,
, , С
, С  . Довести, що трикутник АВС правильний.
. Довести, що трикутник АВС правильний. і
і  .
. і
і  .
. , С
, С  і
і  .
. . Знайти точку В, яка симетрична точці А відносно полюса.
. Знайти точку В, яка симетрична точці А відносно полюса. , Q
, Q  і F
і F  .
. ,
, , С
, С 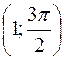 , D
, D  , Е (5; 0). Які координати будуть мати ці точки, якщо повернути полярну вісь біля полюса в додатному напрямку на кут
, Е (5; 0). Які координати будуть мати ці точки, якщо повернути полярну вісь біля полюса в додатному напрямку на кут  .
.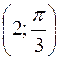 , В
, В  , при чому вісь абсцис співпадає з полярною віссю, а початок координат з полюсом.
, при чому вісь абсцис співпадає з полярною віссю, а початок координат з полюсом.

 ,
,  ,
, 

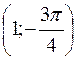 ,
,  ,
,  ,
,  ,
, 

 , D
, D 





 , B
, B  , C
, C  , D
, D  , F
, F 


 , M3
, M3  , M4
, M4  , M5
, M5  , M6
, M6 




 , M4
, M4  , M5
, M5  ,
,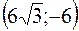

 , M4
, M4  , M5
, M5  , (-4, 1),
, (-4, 1),  ,
, 
 , М3
, М3  , М5
, М5  ,
,
 , Р
, Р 


