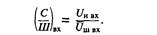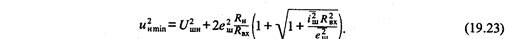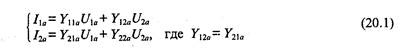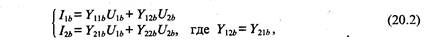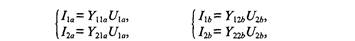и шумы электронных усилителей

Источники шумов. Источниками шумов усилителей являются резистивные эле­менты, а также различные усилительные приборы: транзисторы, электронные лампы, диоды и др. Выбор транзистора или лампы для высокочувствительного усилителя зависит от двух параметров: их собственных шумов и входного сопро­тивления. Собственные шумы входного каскада усилителя определяют его чув­ствительность, а входное сопротивление — условия согласования с источником сигнала.

Собственные шумы резистивных элементов зависят от их сопротивления R или проводимости G и определяются по формуле Найквиста:

где <7iii и/ц, — среднеквадратичные значения напряжения и тока шума, соответ­ственно; k= 1,38-10 ""Дж/К — постоянная Больцмана; Т— абсолютная температу­ра в К; R=G ' сопротивление в омах; Д/— полоса частот в герцах.

Так, например, источник сигнала с внутренним сопротивлением /?„=10к0м при температуре Г=ЗООК и полосе частот А/=10кГц имеет напряжение шума

Мощность тепловых шумов сопротивления не зависит от значения сопротив­ления и определяется по формуле

В полосе частот А/=10кГц мощность тепловых шумов равна

В транзисторах и электронных лампах действуют три основных вида шумов:

1) полный дробовый шум, вызываемый током утечки управляющего электродаj (затвора транзистора или сетки лампы), 2) дробовый шум анодного тока лампы

или тепловой шум проводящего канала транзистора, 3) генерационно-рекомбина-[ ционный шум транзистора или шум мерцания катода лампы (фликкер-шум). Ток дробового шума управляющего электрода определяется выражением

где /о — ток управляющего электрода; q =1,6-10 "Кл — заряд электрона, Д/— полоса частот.

В электронных лампах, которые работают с отрицательным напряжением смещения на сетке, ток утечки сетки имеет значение 10"¹⁰... Ю^А. В полевых транзисторах с управляющим ^-и-переходом ток утечки лежит в пределах 10'⁸...10'¹¹A. В полевых транзисторах с изолированным затвором ток утечки зат­вора очень мал и составляет 10"¹³... КГ^А. В биполярных транзисторах ток базы сравнительно велик и лежит в пределах 10'⁶... Ю^А.

Тепловой шум проводящего канала транзистора и дробовый шум анодного тока лампы приблизительно равны шуму, создаваемому сопротивлением Д'эк> и напряжение теплового шума определяется выражением

Генерационно-рекомбинационньш шум транзистора и шум мерцания катода лампы имеют зависимость вида \/f. Полное напряжение шума определяется по формуле:

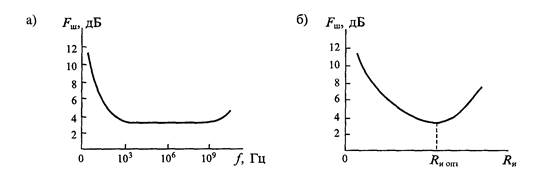
Выражение (19.5) показывает, что напряжение шума растет при понижении частоты и на частоте /, напряжение тепловых шумов (19.4) становится равным напряжению низкочастотных шумов.

Коэффициент шума усилителя. Для оценки шумовых свойств ламп, транзисто­ров и усилителей в целом можно пользоваться эквивалентным напряжением шумов, эквивалентным сопротивлением шумов или коэффициентом шума. Наибо­лее универсальным шумовым параметром является коэффициент шума, который позволяет определять и сравнивать по единой методике шумовые свойства тран­зисторов, ламп и усилителей в зависимости от частоты, внутреннего сопротивле­ния источника сигнала и др.

Расчет коэффициента шума усилителя можно производить с помощью эквива­лентных генераторов шума холостого хода и короткого замыкания. Эта методика основана на замене шумящего усилителя нешумящим, на входе которого включе­ны генераторы шумового тока ^, и напряжения ё~ш. Схема такой замены приведена на рис. 19.1.

Такой подход имеет определенные преимущества, поскольку величины экви­валентных входных шумов могут быть измерены. Коэффициент шума и оптималь­ное сопротивление источника сигнала также можно выразить через эти два пара­метра. Значения ё^тиТ^ можно определить независимо друг от друга. Для опре­деления e„i выходной шум усилителя при коротком замыкании на входе

Рис. 19.1. Эквивалентная схема шумящего (а) и нешумящего (б) усилителя

сравнивается с выходным напряжением, производимым малым известным вход­ным напряжением. Для определения i^ выходной шум усилителя при разомкнутом входе сравнивается с выходным напряжением, производимым малым известным током на входе. Оба источника ёщ и г'ш могут быть введены в схему усилителя с обратной связью без изменения значения. По этой причине значения шумовых генераторов почти не зависят от схемы включения транзистора или лампы, а оп­ределяются только их типом и режимом работы.

Коэффициент шума усилителя определяется отношением полной мощности шумов./^.вых на выходе усилителя (исключая шумы нагрузки) к той части шумов на выходе, которая вызвана тепловыми шумами сопротивления источника сигна­ла ршилых-

где /'ши=4^ГД/ — мощность шумов сопротивления источника сигнала, Рщу — мощность шумов усилителя на входе, Кр — коэффициент усиления по мощности. Мощность шумов на входе усилителя можно определить по формуле '

где 0 < р < 1 — коэффициент корреляции шумов е^ и /щ; если источники шумов е^ и;ц, независимы, то р = 0, при их тесной взаимной зависимости р = 1.

Из формулы (19.7) можно определить оптимальное сопротивление источника сигнала, при котором коэффициент шума становится минимальным:

откуда

Определение коэффициента корреляции шумов р можно производить по фор­муле (19.8), измеряя значение jF'm.min при оптимальном сопротивлении источника сигнала.Ки.опт- Если же сопротивление источника сигнала сделать много больше или много меньше оптимального значения, то коэффициент шума будет зависеть только от одного из двух генераторов шума. Для каждого сопротивления источ­ника сигнала можно определить коэффициент шума, пользуясь вычисленными или измеренными значениями е~щ и 1щ по формуле (19.7).

Поскольку для транзисторов и электронных ламп корреляция шумов ещ и i^ весьма мала, то р^О, и коэффициент шума можно определять по формуле

где u^y=e'^+i^R^ — напряжение шума, приведенное к входу усилителя.

В справочной литературе обычно приводятся значения полного напряжения шума «ш при заданном сопротивлении источника сигнала или коэффициент шума ^m.min- Типовые зависимости коэффициента шума от частоты и сопротивления источника сигнала приведены на рис. 19.2. Если известно значение коэффициента шума усилителя (или входного транзистора), то при заданном значении сопротив­ления -R„ источника сигнала можно определить напряжение шума, приведенное ко входу усилителя по формуле

Для нешумящего усилителя г<щ=0, что соответствует минимальному значению коэффициента шума F=1. Обычно коэффициент шума оценивают в децибелах, поэтому для нешумящего усилителя Р=ОдБ.

Предельная чувствительность усилителя. Предельную чувствительность уси­лителя принято оценивать отношением сигнал-шум:

где С/и — действующее значение напряжения источника сигнала, С/щ — средне­квадратичное (действующее) значение напряжения шума.

Принято считать, что минимальный уровень сигнала [/„mm определяется из условия

Отсюда следует, что без усилителя минимально различимый сигнал определя­ется напряжением шума сопротивления источника, т. е. t/пцп = С/щи.

Рис. 19.2. Типовые зависимости коэффициента шума от частоты (а) и сопротивления источника сигнала (б)

Шум усилителя изменяет отношение (С/Я/),;, на отношение (С/Л7),ых. Это из­менение отношения сигнала и шума оценивают при помощи коэффициента шума, рассмотренного выше:

где и^^ых^ U^+U^y — мощность шума на выходе усилителя, г/^„=4^Г^„Д/— мощность_шума сопротивления источника сигнала. После подстановки значений ^1вых и £/^,x получим

что совпадает с уравнением (19.У).

Найдем отношение сигнал — шум на выходе усилителя, пользуясь уравнени­ем (19.12)

Для определения минимально допустимого сигнала источника положим, что (С1Ш)^=\ и из уравнения (19.14) найдем:

Уравнение (19.15) определяет предельную чувствительность усилителя в виде уровня минимального входного сигнала источника, при котором на выходе усилите­ля выполняется условие равенства напряжения сигнала напряжению шума. Из этого уравнения следует, что при расширении полосы пропускания усилителя и увеличения его коэффициента шума предельная чувствительность усилителя ухудшается.

Построение малошумящих усилителей. При построении малошумящих усили­телей приходится решать несколько проблем:

• выбор усилительного элемента: биполярный или полевой транзистор, элек­тронная лампа, операционный усилитель и др.;

• выбор режима работы усилительного элемента: напряжения питания, тока коллектора или стока и др.;

• возможность согласования сопротивления источника сигнала по шумам.

Рассмотрим построение малошумящих усилителей на биполярных транзисто­рах. Схема усилителя на биполярном транзисторе с учетом источников шума при­ведена на рис. 19.3 а. На этой схеме транзистор предполагается нешумящим, а его шумы учтены источниками ё~ш и <щ, включенными в цепь базы.

Эту схему можно заменить эквивалентной, если пересчитать источник тока шума 1щ в источник напряжения шума г„Д„ включенный последовательно с ё^, как показано на рис. 19.3 б. Если считать, что эти источники взаимно независимы, то полное напряжение шума будет равно напряжению Иц^У si⁺ Ош-^и)². источник которого включен в схему замещения, приведенную на рис. 19.3 в.

Очевидно, что при малом сопротивлении источника сигнала 7?„-*0, преобла­дает источник напряжения шума Сщ, а при большом сопротивлении R»-*⁰⁰ будет преобладать источник тока шума <ц,.

Рис. 19.3. Моделирование шумящего биполярного транзистора (а), замена источника тока шума (б) и результирующий источник напряжения шума (в)

Для биполярного транзистора спектральная плотность напряжения шума йщ определяется двумя составляющими: тепловым шумом сопротивления базы rg и дробовым шумом коллекторного тока /к> протекающим через сопротивление эмиттера г,, т. е.

где Гэ=(рг/4, a ^=kT/q. Подставив значения г, в формулу (19.16), получим напря­жение источника шума

Таким образом, первый член в формуле (19.17) не зависит от тока коллекто­ра, а второй убывает с ростом тока /к. График зависимости напряжения Сц, от тока коллектора приведен на рис. 19.4 а. В связи с этим для снижения ещ целесообразно повышать ток коллектора до значения 0,1...2мА.

Рис. 19.4. Графики зависимостей напряжения шума (а) и тока шума (б) от тока коллектора для биполярного транзистора

Ток шума г'щ биполярного транзистора порождается дробовым эффектом кол­лекторного тока и определяется формулой

Очевидно, что ток шума растет с ростом тока коллектора, как показано на рис. 19.4 б.

Поскольку е~щ уменьшается, а ТщК^ растет с ростом тока коллектора, то при заданном значении /?„ можно найти оптимальный ток коллектора /к.опт> который соответствует минимуму напряжения шума Мщпцп, как показано на рис. 19.5.

Согласование усилителя с источником сигнала по шумам. Наиболее высокую чувствительность имеют усилители при согласовании источника сигнала с шумя­щим усилителем через входной трансформатор. Схема подключения источника сигнала и„ с внутренним сопротивлением./?„ к усилителю с входном сопротивле­нием 7?ах через согласующий трансформатор приведена на рис. 19.6 а.

При анализе этой схемы будем полагать, что входная емкость усилителя срав­нительно мала, а собственные сопротивления обмоток трансформатора и усилите­ля учтены в эквивалентных источниках бц, и /ц,. Также делается допущение, что

входной трансформатор Тр является идеальным и имеет коэффициент транс­формации п. Такое допущение справед­ливо, если сопротивление первичной об­мотки трансформатора незначительно по сравнению с внутренним сопротивле­нием источника сигнала, а сопротивле­ние вторичной обмотки трансформатора значительно меньше приведенного к вторичной обмотке сопротивления источника сигнала.

Рис. 19.5. Зависимость результирующего напряжения шума от тока коллектора

Рис. 19.6. Согласование источника с шумящим усилителем при помощи трансформатора (а) и его схема замещения (б)

Схема входной цепи с приведенными к вторичной обмотке источниками сиг­нала и шума представлена на рис. 9.6 б. Напряжение сигнала на входе усилителя

Напряжение шума на входе усилителя

Отношение сигнал—шум на входе усилителя определяется уравнением

Предельную чувствительность усилителя можно определить, если положить отношение С/Л/=1, т. е. Ц^.вx⁼ ^ш.вх- Подставив значения (19.19) и (19.20), получим уравнение

откуда найдем

Первый член в уравнении (19.21) определяет абсолютный нижний предел ми­нимального входного сигнала, так как он представляет собой напряжение тепло­вых шумов источника сигнала в полосе пропускания усилителя. Два других члена выражения (19.21) определяют снижение предельной чувствительности усилителя за счет его собственных шумов.

Выбор оптимального коэффициента трансформации позволяет повысить чув­ствительность усилителя и снизить минимальный усиливаемый сигнал. Для опре­деления По„т продифференцируем урав­нение (19.21) по п

откуда найдем

Уравнение (19.22) позволяет при заданном значении собственных шумов усилителя определить оптимальный ко­эффициент трансформации. Подставляя значение (19.22) в уравнение (19.21), найдем минимальный усиливаемый сигнал (19.23)

Рис. 19.7. Зависимость минимального входного напряжения от коэффициента трансформации

На рис. 19.7 приведены графики минимального усиливаемого сигнала при различных значениях коэффициента трансформации и сопротивления источника сигнала. Так, например, если входной трансформатор имеет коэффициент транс­формации п =140 и сопротивление источника сигнала 2?,,= 100 Ом, то минималь­ный усиливаемый сигнал составляет {/„.щи, = 3,7 нВ.

Лекция 20. Активные фильтры

Особенности и назначение активных фильтров. Активный фильтр представ­ляет собой четырехполюсник, содержащий пассивные.КС-цепи и активные элементы: транзисторы, электронные лампы или операционные усилители. Актив­ные фильтры обычно не содержат катушек индуктивности. Стремление исключить катушки индуктивности из фильтра вызвано рядом причин: 1) катушки индуктив­ности имеют большие габариты и массу; 2) потери в катушках приводят к откло­нению расчетных характеристик фильтра от реальных значений; 3) в катушках рассеивается большая мощность; 4) в катушках с сердечником проявляется нели­нейный эффект, связанный с насыщением сердечника. Активные фильтры можно реализовать на повторителях напряжения, на операционных усилителях, на усили­телях с ограниченным усилением и др.

Пассивные частотные фильтры, обычно рассматриваемые в курсе электротех­ники, выполняются на LC- или на /?С-цепях без применения усилительных актив­ных элементов. Такие фильтры не требуют источников питания и имеют простое исполнение, однако они не обеспечивают хорошего разделения полосы пропуска­ния от полосы затухания; в области пропускания и затухания могут наблюдаться большие неравномерности передаточной характеристики; очень сложно выпол­нить условие согласование фильтра с нагрузкой.

В отличие от пассивных, активные фильтры обеспечивают более качественное разделение полос пропускания и затухания. В них сравнительно просто можно регулировать неравномерности частотной характеристики в области пропускания и затухания, не предъявляется жестких требований к согласованию нагрузки с фильтром. Все эти преимущества активных фильтров обеспечили им самое ши­рокое применение.

Классификация активных фильтров. Активные фильтры можно разделить на группы по различным признакам: назначению, полосе пропускаемых частот, типу усилительных элементов, виду обратных связей и др. По полосе пропускаемых частот фильтры делятся на четыре основные группы: нижних частот, верхних ча­стот, полосовые и заграждающие. Фильтры нижних частот пропускают сигналы от постоянного напряжения до некоторой предельной частоты, называемой часто­той среза фильтра. Фильтры верхних частот, наоборот, пропускают сигналы, начиная с частоты среза и выше. Полосовые фильтры пропускают сигналы в некоторой полосе частот от/i до/г> а заграждающие фильтры имеют характери­стику, противоположную полосовым, и пропускают сигналы с частотой ниже /i и выше /г. Как полосовые, так и заграждающие фильтры могут иметь гребенча­тую частотную характеристику, в которой будет несколько полос пропускания и затухания.

По назначению фильтры делятся на сглаживающие фильтры источников питания, заграждающие фильтры помех, фильтры для селективных усилителей низкой или высокой частоты и др.

По типу усилительных элементов можно выделить транзисторные фильтры, фильтры на усилителях с ограниченным усилением, на операционных усилителях, на повторителях напряжения и др. Все рассмотренные фильтры могут иметь одну цепь обратной связи или несколько. В связи с этим различают фильтры с одно­контурной и с многоконтурной обратной связью. Кроме этого, различают фильт­ры по числу полюсов на частотной характеристике — фильтры первого порядка, второго и более высоких порядков. Фильтры высоких порядков имеют более кру­тые границы полос пропускания и затухания и более плоскую характеристику в области полосы пропускания. К таким фильтрам относятся фильтры Чебышева, Баттерворта, Бесселя и др. '

Широкие возможности активных.RC-фильтров связаны с использованием в них активных элементов. Цепи, содержащие только сопротивления и емкости, имеют полюсы передаточной функции на отрицательной действительной полуоси комплексной плоскости p=c+j(u, что ограничивает возможности создания филь­тров. В отличие от пассивных, активные /iC-фильтры (.^.КС-фильтры) могут иметь полюсы в любой части комплексной плоскости. Однако схемы с полюсами в правой полуплоскости неустойчивы, поэтому в активных фильтрах используют­ся только те схемы, полюсы передаточной функции которых располагаются в ле­вой полуплоскости или на оси jw.

Активные фильтры на операционных усилителях с одноконтурной обратной связью. Схема активного фильтра на ОУ с одноконтурной обратной связью при­ведена на рис. 20.1. Она состоит из двух пассивных четырехполюсников А и В и операционного инвертирующего усилителя ОУ. Четырехполюсник А включен между входом фильтра и входом операционного усилителя, а четырехполюсник В включен в цепи обратной связи между входом и выходом ОУ. При анализе схем будем считать ОУ идеальным и инвертирующим.

Передаточную функцию для схемы, приведенной на рис. 20.1, можно полу­чить, используя уравнения четырехполюсников в У-параметрах:

и

Рис. 20.1 Схема активного фильтра на ОУ с одноконтурной обратной связью

где Гц =^ у,=о — проводимость обратной передачи при коротком замыкании на

входе, уз! ^{= t/" c/2=o — проводимость прямой передачи при коротком замыкании на выходе.}

Поскольку для идеального ОУ и^=0 и i^=0, то u^u^Q', iia^-hb и уравне- I ние (20.1) и (20.2) упрощаются и приводятся к виду

откуда получаем, что

Из уравнения (20.3) найдем коэффициент передачи фильтра по напряжению

который определяется отношением передаточных проводимостей пассивных четы­рехполюсников А и В.

Так как четырехполюсники А и В пассивные, то их полюсы лежат на отрица­тельной части действительной полуоси комплексной плоскости р. Если обе цепи имеют одинаковые полюсы, то знаменатели функций Y^ и Y^i, сократятся и их полюсы не будут влиять на коэффициент передачи фильтра. В этом случае полю­сы передаточной функции (20.4) будут определяться нулями передаточной про­водимости К|2д. При этом, поскольку нули передаточной проводимости пассивной 7?С-цепи могут лежать в любой точке комплексной плоскости р, оказывается возможным реализовать цепь с коэффициентом передачи, имеющим комплексно-сопряженные полюсы, как для колебательного контура. Однако для обеспечения устойчивости схемы эти полюсы должны лежать в левой части комплексной плоскости, т. е. вещественная часть комплексного полюса должна быть отрица­тельной.

Подобным же образом можно утверждать, что нули коэффициента передачи (20.4) будут определяться нулями передаточной проводимости Г^д и, следователь­но, можно получить любые требуемые действительные или комплексно-сопряжен­ные нули коэффициента передачи фильтра. Таким образом, активный.КС-фильтрс одноконтурной обратной связью в цепи идеального ОУ дает возможность полу­чать коэффициент передачи практически с любыми нулями и полюсами.

Некоторые пассивные.RC-цепи, используемые в активных фильтрах, приведе­ны в табл. 20.1.

Фильтр нижних частот (ФНЧ) с одноконтурной обратной связью предназначен для выделения сигналов, частота которых ниие некоторой заданной частоты, называемой частотой среза фильтра. ФНЧ практически без ослабления пропуска­ет сигналы в полосе частот от постоянного напряжения до частоты среза и ослаб­ляет сигналы, частота которых выше частоты среза.

В зависимости от числа полюсов в передаточной характеристике ФНЧ делят на однополюсные (первого порядка), двухполюсные (второго порядка) и многопо­люсные (высокого порядка). Схема ФНЧ первого порядка приведена на рис. 20.2 а. В этом фильтре четырехполюсник А выполнен на одном сопротивле­нии Га, а четырехполюсник В содержит параллельно соединенные элементы г<, и Сь. Передаточная проводимость четырехполюсника А имеет значение Y^=-ga, а че­тырехполюсника В — значение Y^'=-{gi,+jwCi,).

Коэффициент передачи ФНЧ по напряжению

.где Ko=ga/gb — коэффициент передачи фильтра на постоянном напряжении, (0(.=g6/Cf, частота среза фильтра.

Модуль передаточной функции фильтра на синусоидальном сигнале равен

а его график приведен на рис. 20.2 б, откуда видно, что на частоте среза фильтр вносит затухание, равное 0,707 Кц (или ЗдБ).

Коэффициент передачи ФНЧ второго порядка в общем случае определяется выражением

где Ко — коэффициент передачи фильтра на постоянном напряжении, со,: — часто­та среза фильтра, o.=Q ' — затухание фильтра, Q — его добротность. Выражение (20.7) имеет два полюса

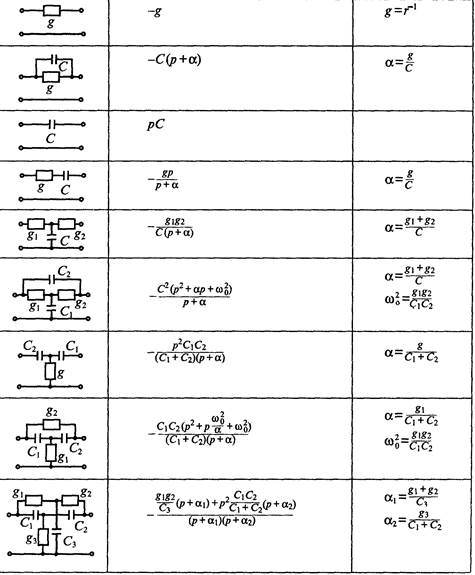
откуда следует, что при ст<2 полюсы коэффициента передачи будут комплексно-сопряженными, а при й>2 — вещественными. Амплитудно частотные характерис­тики ФНЧ второго порядка для различных значений ос<2 приведены на рис. 20.3 а. При а-* 0 добротность б—⁰⁰ и фильтр будет возбуждаться на частоте (Ос.

Практическая реализация ФНЧ второго порядка возможна при использова­нии в качестве четырехполюсников А и В звеньев 5 и 6 из табл. 20.1. Схема такого Таблица 20.1 Пассивные четырехполюсники для активных фильтров Таблица 20.1

 

№

Схема цепи

Передаточная проводимость У^!

Параметры

 

Рис. 20.2. Фильтр нижних частот с одноконтурной обратной связью первого порядка (а) и его амплитудпо-частотная характеристика (б)

фильтра приведена на рис. 20.3 б. При этом в соответствии с табл. 20.1 частота среза определяется выражением

добротность фильтра

а коэффициент передачи на постоянном напряжении

Фильтр верхних частот (ФВЧ) с одноконтурной обратной связью предназна­чен для выделения сигналов, частота которых выше некоторой заданной частоты, называемой частотой среза фильтра. ФВЧ практически без ослабления пропускает сигналы выше частоты среза и ослабляет сигналы с частотой ниже частоты среза.

Рис 20.3. Амплитудно-частотная характеристика ФНЧ второго порядка (а) и его схема (б)

В зависимости от числа полюсов в передаточной характеристике ФВЧ делят на однополюсные (первого порядка) и двухполюсные (второго порядка). Схема ФВЧ первого порядка приведена на рис. 20.4 а. В этой схеме изменен только четы­рехполюсник А, в котором сопротивление Гд заменено емкостью С„. Передаточные проводимости пассивных четырехполюсников имеют значения

Коэффициент передачи фильтра определяется по формуле (20.4) и равен

где Ku=C„/Ci, — коэффициент передачи фильтра на бесконечно высокой частоте (й-* оо)^ (й^=(гьСь) ' — частота среза фильтра.

Амплитудно-частотная характеристика ФВЧ первого порядка приведена на рис. 20.4 б. На частоте среза фильтра коэффициент передачи фильтра достигает значения 0,707А'о-

Передаточная характеристика ФВЧ второго порядка определяется в общем случае выражением

которое имеет два полюса

Амплитудно-частотная характеристика такого фильтра определяется фор­мулой

и имеет вид, изображенный на рис. 20.5 а.

При значении а<2 полюсы коэффициента передачи ФВЧ являются комплекс­но сопряженными, а при а>2 — вещественными. Для получения максимально

Рис. 20 4. Схема фильтра верхних частот первого порядка с одноконтурной обратной связью (а) и его амплитудно-частотная характеристика (б)

гладкой характеристики ФВЧ обычно выбирают oc=V2. При этом наклон характе­ристики составляет 40 дБ на декаду.

Практическая схема ФВЧ второго порядка приведена на рис. 20.5 б. Она по­лучена при использовании в качестве четырехполюсников А и В- звеньев 7 и б, приведенных в табл. 20.1. В соответствии с характеристиками звеньев фильтра основные характеристики ФВЧ определяются выражениями:

• частота среза фильтра:

• коэффициент передачи на высокой частоте:

• добротность:

Полосовой фильтр с одноконтурной обратной связью (ПФ) предназначен для выделения сигналов, частота которых лежит в пределах некоторой полосы tt)oi<co<(0o2. При этом он практически без ослабления пропускает сигналы, лежа­щие в этой полосе, и ослабляет сигналы, частоты которых лежат за пределами полосы пропускания.

Полосовые фильтры бывают двухполюсные (второго порядка) и многополюс­ные (высокого порядка). Передаточная характеристика ПФ второго порядка оп­ределяется выражением

которое имеет два комплексно сопряженных полюса C0oi и йог.

Рис. 20.5. Амплитудно-частотная характеристика ФВЧ второго порядка (а) и его схема (б)