Решение. Потенциальная энергия балки с пружиной
Потенциальная энергия балки с пружиной
где P сила, возникшая от перемещения
Запишем баланс энергии
Отсюда критическое перемещение опорной точки пружины равно
Для ответа на второй вопрос надо вычислить вторую вариацию внутренней энергии и посмотреть её знак (больше нуля устойчивый рост, меньше - неустойчивый). Для этого следует взять вторую производную.
Безразличное состояние критического равновесия будет при
Неустойчивый рост трещины при Устойчивой трещина будет, если Переход из устойчивого состояния в неустойчивое зависит от соотношения между жесткостью пружины (жесткость обратно пропорциональна податливости) и жесткостью консоли.
|
,
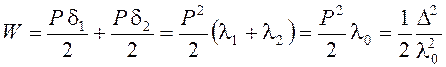, которое остается фиксированным при возможном росте трещины. Прогиб балки 
, следовательно, податливость балки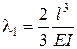 
(длина балки равна длине трещины). Удлинение пружины 
, где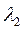 
- податливость пружины (заданная величина).
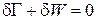или более подробно (
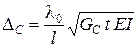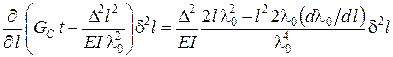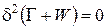сократили)
.
.
.
или
. Напомним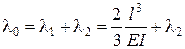 
.
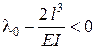или 
. Если податливость пружины удовлетворяет этому условия (пружина жесткая), то трещина при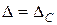 
станет ускоренно распространяться.
или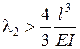 
(пружина податливая, мягкая). По достижении критического состояния трещина будет расти устойчиво с ростом задаваемого перемещения точки крепления пружины.
