Энергетический критерий Гриффитса
[1] Понятие трещиностойкости стоит в одном ряду с такими понятиями механики материалов,как пластичность, прочность, ползучесть и т.п. Эти понятия отражают явления, происходящие с материалом, и реакцию материала на внешнее воздействие. Мера количественной оценки этой реакции может быть измерена разными величинами. Например, для тела с трещиной характеристики трещиностойкости можно оценивать критическим коэффициентом интенсивности напряжений, пределом трещиностойкости, критическим раскрытием вершины трещины, удельной работой разрушения, критическим значением "джей"-интеграла, процентом волокна в изломе, критической температурой хрупкости, ударной вязкостью образца с трещиной и др. Энергетический критерий Гриффитса
Обратимся теперь к энергетическому критерию разрушения, предложенному Аланом Гриффитсом. Появившиеся в 1921 и 1924 годах работы Гриффитса по теории трещин считаются основополагающими, которые открыли путь для теоретических исследований в области механического разрушения[1]. Кратко ее содержание сводится к тому, что при продвижении трещины на единицу площади (при этом образуются две ее поверхности) выделяющаяся энергия упругой деформации G расходуется на образование этой единицы площади. Тогда критерий разрушения принимает вид
Здесь символом Гриффитсом была решена следующая задача. Дана неограниченная плоскость (развертка цилиндрической поверхности трубы), ослабленная одиночной прямолинейной трещиной (в виде предельно тонкой эллиптической полости) Предполагается, что растяжение в направлении линии трещины (вдоль оси В результате наличия трещины, потенциальная энергия W пластинки (единичной толщины и на единицу площади трещины) уменьшается на величину G = Здесь Компоненты перемещения точки на поверхности разреза (при
Отсюда видно, что поверхность разреза в результате деформации (пренебрегая компонентой u) принимает форму эллипса Для плоского напряженного состояния Поставив полученные величины в критерий разрушения (3.7.1) находим критическое (разрушающее) напряжение (формула Гриффитса)
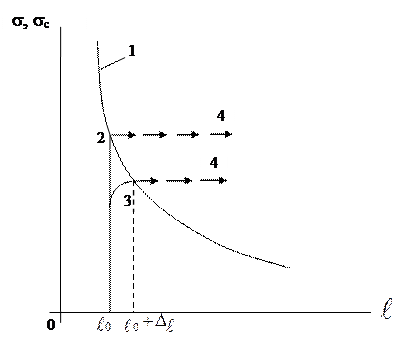
Последнее равенство написано на основании эквивалентности энергетического и силового критериев (см. раздел 3.8). Уравнение (3.7.3) показывает, что критическая диаграмма разрушения (связь разрушающего напряжения с длиной трещины) имеет вид гиперболы – чем длиннее трещина, тем меньше разрушающее напряжение (рис. 3.22, линия 1). Критическое состояние равновесия в данной задаче неустойчиво, что видно из того, что Стремление длины трещины к нулю приводит к бесконечной прочности тела, что физически нереально. Это естественно, если вспомнить постановку задачи – тело теряет прочность только из-за наличия трещины. Поэтому эта теория ограничена со стороны малых длин трещин и, соответственно, со стороны больших напряжений. Ориентировочно пригодность критерия определяется неравенством
Рис. 3.22. Критическая диаграмма разрушения в задаче Гриффитса
Этой теорией не учитывается медленный докритический рост трещины, который наблюдается экспериментально. В действительности быстрый рост трещины (линии 4 на рис. 3.22) наступает не внезапно (линия 2), а после предварительного медленного устойчивого роста (линия 3). Докритический рост трещины (на величину В последствии Гриффитсом было отмечено, что представляет интерес не только величина критического напряжения, но также и максимальное напряжение у вершины трещины (1924). Это напряжение можно оценить, если известен радиус закругления в конце трещины. Тогда, максимальное напряжение определяется выражением
где
|

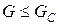 (3.7.1)
(3.7.1)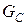 обозначена удельная (т.е. на единицу площади) работа разрушения или, иначе, вязкость разрушения. Знак равенства в (3.7.1) означает наступление критического (разрушающего) состояния.
обозначена удельная (т.е. на единицу площади) работа разрушения или, иначе, вязкость разрушения. Знак равенства в (3.7.1) означает наступление критического (разрушающего) состояния.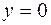 ,
, 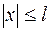 . Плоскость растягивается равномерным на бесконечности напряжением
. Плоскость растягивается равномерным на бесконечности напряжением 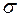 в направлении оси
в направлении оси 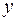 (перпендикулярно линии трещины, см. рис. 3.4).
(перпендикулярно линии трещины, см. рис. 3.4).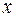 ) не оказывает влияния на условия распространения трещины[2]. Требуется установить, при каком значении внешнего напряжения
) не оказывает влияния на условия распространения трещины[2]. Требуется установить, при каком значении внешнего напряжения 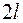 станет неустойчивой, т.е. начнет быстро распространяться при постоянной внешней нагрузке.
станет неустойчивой, т.е. начнет быстро распространяться при постоянной внешней нагрузке.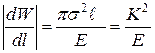
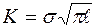 - коэффициент интенсивности напряжений.
- коэффициент интенсивности напряжений.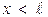 ) случае плоского напряженного состояния будут
) случае плоского напряженного состояния будут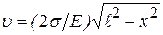 ,
, 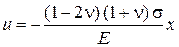 (3.7.2)
(3.7.2)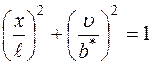 ,
,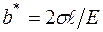 (перемещение в середине трещины).
(перемещение в середине трещины).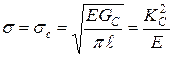 (3.7.3)
(3.7.3) и трещина, выйдя из критического состояния, неудержимо растет с положительным ускорением, стремясь к максимально возможной скорости в данной упругой среде. По Н.Ф. Мотту (1948) скорость роста трещины в закритическом (l > l C) состоянии равна
и трещина, выйдя из критического состояния, неудержимо растет с положительным ускорением, стремясь к максимально возможной скорости в данной упругой среде. По Н.Ф. Мотту (1948) скорость роста трещины в закритическом (l > l C) состоянии равна  .
.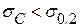 .
.
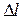 ) может быть объяснен, если принять во внимание наличие пластической зоны перед концом трещины. При этом в удельную работу разрушения включается работа пластических деформаций вокруг вершины трещины и тогда суммарная удельная работа разрушения оказывается функцией длины трещины, что и предопределяет возникновение докритической стадии роста трещины. Для описания докритического роста трещины введено понятие R - кривых (см. раздел 4.6).
) может быть объяснен, если принять во внимание наличие пластической зоны перед концом трещины. При этом в удельную работу разрушения включается работа пластических деформаций вокруг вершины трещины и тогда суммарная удельная работа разрушения оказывается функцией длины трещины, что и предопределяет возникновение докритической стадии роста трещины. Для описания докритического роста трещины введено понятие R - кривых (см. раздел 4.6).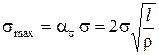 ,
,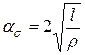 коэффициент концентрации напряжения (взятый из упомянутого решения Инглиса), r - радиус закругления в вершинах эллиптической трещины. Оценим поверхностную энергию тела. Положим напряженное состояние у вершины трещины одноосным с напряжением равным теоретической прочности
коэффициент концентрации напряжения (взятый из упомянутого решения Инглиса), r - радиус закругления в вершинах эллиптической трещины. Оценим поверхностную энергию тела. Положим напряженное состояние у вершины трещины одноосным с напряжением равным теоретической прочности 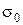 . Энергия деформации в единице объема
. Энергия деформации в единице объема 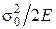 . Пусть решетка простая кубическая, тогда энергия, запасенная в ячейке и отнесенная к единице площади, даст удельную поверхностную энергию
. Пусть решетка простая кубическая, тогда энергия, запасенная в ячейке и отнесенная к единице площади, даст удельную поверхностную энергию 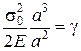 . Здесь а – параметр решетки.
. Здесь а – параметр решетки.  Положив, что максимальное напряжение у вершины трещины
Положив, что максимальное напряжение у вершины трещины 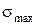 равно теоретической прочности
равно теоретической прочности 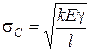 . Здесь принято, что радиус кривизны в вершине трещины пропорционален параметру решетки
. Здесь принято, что радиус кривизны в вершине трещины пропорционален параметру решетки 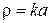 . Полученные соотношения показывают, что одновременно с необходимым условием разрушения – энергетическим, удовлетворяется также и достаточное - силовое
. Полученные соотношения показывают, что одновременно с необходимым условием разрушения – энергетическим, удовлетворяется также и достаточное - силовое 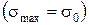 .
.


