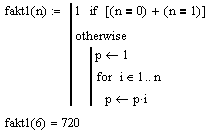Условный оператор if и оператор otherwise. Рассмотрим пример программного блока, вычисляющего факториал с использованием рекурсии

| В данном примере 1 возвращается, только если n=0 или n=1. Обратите внимание на задание некольких условий - со знаком плюс, каждое условие в скобках. В остальных случаях, учитывая формулу n!=n*(n-1)!, вызывается fakt(n-1) и умножается на n. При помощи функции error можно вывести сообщение об ошибке при неправильном вводе аргумента.
|
Для демонстрации работы цикла for рассмотрим ту же задачу, но вычисление факториала осуществим при помощи цикла.
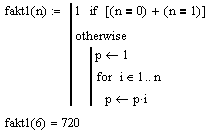
| Если n=0 или n=1, возвращается 1, в противном случае при помощи цикла for вычисляется произведение n!=1*2*3...*n. Вычисленное последним значение p возвращается автоматически.
|
| В следующем примере при помощи алгоритма Евклида определяется наибольший общий делитель. Для реализации алгоритма используется цикл с ключевым словом while
| 
|
Прерывание цикла при помощи операторов break и continue. Оператор return. Первый пример - релизация метода касательных Ньютона для определения нулей функции. На основе начального значения x вычисляется новое улучшенное значение x, расположенное ближе к искомому нулю функции. При этом итерации повторяются до тех пор, пока значение функции не станет меньше заданной точности (в примере 10-6).

| При помощи оператора return организовано завершение программы в нужный момент. В данном примере если число итераций больше или равно 10, то происходит прерывание программы и выдается сообщение о том, что слишком много итераций. Здесь также отслеживаются случаи, когда производная в знаменателе близка к нулю и выдается об этом сообщение.
|
| Кроме ключевого слова break имеется ключевое слово continue с похожей функцией. В то время как break прерывает цикл и осуществляет переход к следующему за циклом оператору, continue прерывает выполнение только текущей итерации.
В примере справа ключевое слово continue используется для выявления всех нулей функции на заданном интервале. При этом в примере производится разбиение интервала на n равных подинтервалов и ищутся те из них, на которых функия меняет знак. При обнаружении такого поинтервала вызывается функия, реализующая метод касательных Ньютона, с начальным значением, находящимся в середине подинтервала.
| 
|
Обратите внимание, по завершении работы программы выдается вектор значений.
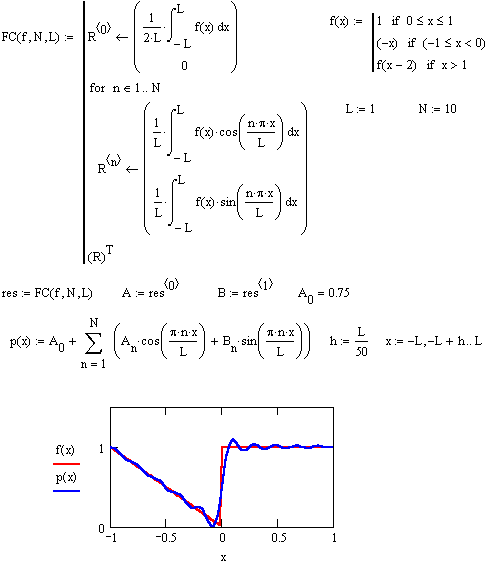
Ниже приводится программа, вычисляющая коэффициенты Фурье функции, причем в результате выдается матица значений: нулевая по счету строка содержит коэффициенты Аn, а первая - коэффициенты Bn. Для выделения этих коэффициентов выдавемая матрица транспонируется и из нее выбирается нулевой столбец для коэффициентов Аn, и первый - для Bn.