Оценка погрешности косвенных измерений
Результат косвенных измерений вычисляется по расчетной формуле, куда обычно входят как табличные величины, так и величины, полученные при прямых измерениях. Каждая из них имеет свою погрешность, а задача состоит в том, чтобы учесть их влияние на погрешность конечного результата. Существуют математические приемы, с помощью которых из расчетной формулы выводится функция для вычисления погрешности косвенных измерений. Эти приемы различны в зависимости от вида расчетной формулы, которая может содержать либо только сомножители, либо еще и слагаемые. Чтобы эти действия были более наглядны, возьмем в качестве примера формулу для определения ускорения, а при равноускоренном движении без начальной скорости, которая содержит только сомножители,
где S – путь, t – соответствующее время. 1. Логарифмируем расчетную формулу:
2. Берем дифференциал от левой и правой части. Напомним, что дифференциал какой-либо величины y – это ее изменение dy при бесконечно малом изменении аргумента dx, а производная некоторой функции – это отношение дифференциалов функции и аргумента, т.е.
3. Заменяем дифференциалы величин на соответствующие абсолютные погрешности, а также все знаки «минус» меняем на знак «плюс», т.е. относительные погрешности только складываются:
Обычно путь S является однократным измерением (задается самим экспериментатором), а соответствующее время t измеряется несколько раз. Погрешность Δ t вычисляется по формуле (1.10), а в знаменатель (1.13) подставляется среднее время á t ñ. Получим среднее значение ускорения á a ñ, подставив в формулу (1.11) среднее время á t ñ и соответствующий ему путь S. Максимальная абсолютная погрешность ускорения определяется из (1.13):
Формула (1.14) указывает на оптимальную методику проведения измерений, т.е. на достижение максимальной точности определения ускорения. Для этого время надо измерять точнее, чем путь, так как отно-сительная погрешность времени входит в формулу (1.14) с коэффициентом2. Если расчетная формула содержит как сомножители, так и слагаемые, то вычисляется сначала максимальная абсолютная погрешность косвенного измерения. Используем в качестве примера формулу для измерения потенциальной энергии шарика массой m, падающего с высоты Н1 до отметки Н2: W = mg (H1 – H2), (1.15) где g – ускорение свободного падения. Для получения формулы вычисления ошибки измерений проделаем следующие операции: 1. Возьмем дифференциал от расчетной формулы: dW = g (H1 – H2) dm + m (H1 – H2) dg + mg (dH1 – dH2). (1.16) 2. Заменим дифференциалы на соответствующие абсолютные погрешности, а также знаки «минус» между дифференциалами на знаки «плюс». Получаем: Δ W = g (H1 – H2) Δ m + m (H1 – H2) Δ g + mg ( Δ H1 + Δ H2). (1.17) 3. Делим левую и правую части на расчетную формулу. Поделим выражение (1.17) на (1.15), получим относительную погрешность измерения:
Из формулы (1.15) следует, что с максимальной точностью следует измерять высоты Н1 и Н2, так как относительная погрешность есть результат деления на малую величину разности (Н1 – Н2). В этой формуле величины m, Н1, Н2 являются результатами однократных измерений, а ускорение свободного падения g – табличной величиной.
|

 , (1.11)
, (1.11) .
. . Отсюда следует, что дифференциал функции равен
. Отсюда следует, что дифференциал функции равен 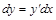 . Кроме того, производная от функции
. Кроме того, производная от функции  равна
равна  , а дифференциал суммы равен сумме дифференциалов. В результате дифференцирования получаем:
, а дифференциал суммы равен сумме дифференциалов. В результате дифференцирования получаем: . (1.12)
. (1.12) . (1.13)
. (1.13)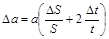 . (1.14)
. (1.14) . (1.18)
. (1.18)


