Оценка величины случайной погрешности
Случайные погрешности являются следствием случайных, неконтролируемых помех, влияние которых на процесс измерения невозможно учесть непосредственно, проявляются в хаотическом изменении результатов повторных наблюдений, могут отклонять результаты измерения от истинного значения в обе стороны. При обработке результатов эксперимента возникают два вопроса: 1) как найти из полученных значений наиболее вероятное значение измеряемой величины и 2) чему равна ожидаемая погрешность измерений? Ответ на эти вопросы дается теорией вероятностей. Согласно этой теории, случайные погрешности измерений подчиняются закону нормального распределения Гаусса. Смысл закона Гаусса заключается в следующем. Допустим, мы хотим измерить некоторую физическую величину, истинное (и нам неизвестное) значение которой есть хо. Проведя несколько раз измерения, вместо хо получаем набор значений х1, х2,… хi,… xn. Оказывается, что с помощью закона распределения мы хотя и не можем указать точное значение хо, но можем найти, с какой вероятностью Р величина хо окажется в любом интервале значений а<xo<b. Область значений а<xo<b называют доверительным интервалом. По закону Гаусса эта вероятность определяется функцией плотности распределения
и равна
Функция плотности распределения f(x) характеризует число случаев, когда измеряемая величина попала в интервал от x до x+dx (dx – малое изменение измеряемой величины). x – набор значений, которые мы получаем в результате измерения, á x ñ – их среднее арифметическое, а
Рис. 1.1
Как видно из рис.1.1, гауссова кривая, имеющая на графике симметричный колоколообразный вид, характеризуется двумя параметрами: положением вершины á x ñ и шириной 2σ; – расстоянием между точками перегиба. Значение á x ñ обычно принимают за ту величину, которую надо было измерить, а σ; характеризует степень влияния случайных погрешностей на результаты измерения: чем меньше σ;, тем уже гауссова кривая и тем, следовательно, точнее проведено измерение. Площадь под кривой от а до b определяет долю случаев, в которых измеряемая величина лежит в этом интервале (т.е. вероятность того, что измеряемая величина попала в интервал от а до b). Следует подчеркнуть, что á x ñ – не истинное значение измеряемой величины, а лишь некоторое приближение к нему. Чем более широким выбирается доверительный интервал, тем выше вероятность попадания истинного значения в этот интервал. Так, например, вероятность отклонения истинного значения от положения вершины гауссовой кривой á x ñ не более чем на σ; равна 0,683, а не более чем на 2σ; – 0,955. Бесконечное увеличение числа измерений не дает заметного увеличения точности. Зависимость надежности (вероятности) от числа измерений сложна и не выражается в элементарных функциях. Существуют специальные таблицы коэффициентов Стьюдента, по которым можно определить, во сколько раз надо увеличить стандартный доверительный интервал S á x ñ, чтобы при определенном числе измерений n получить требуемую вероятность (надежность) Р. Стандартный доверительный интервал, или среднеквадратичная погрешность среднего, согласно выводам математической статистики убывает пропорционально
Таблица 1.1 Таблица коэффициентов Стьюдента t (P,n)
Чтобы найти величину случайной погрешности, необходимо стандартный доверительный интервал умножить на коэффициент Стьюдента: Δ хсл.= t (P,n) . S á x ñ. (1.9)
|

 (1.4)
(1.4) . (1.5)
. (1.5) среднее квадратичное отклонение
среднее квадратичное отклонение , (1.6)
, (1.6) . (1.7)
. (1.7)
 и определяется формулой
и определяется формулой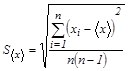 . (1.8)
. (1.8)



