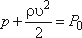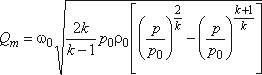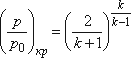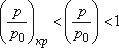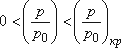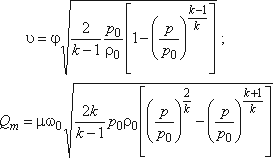Течение воздуха
Инженерные расчеты пневмосистем сводятся к определению скоростей и расходов воздуха при наполнении и опорожнении резервуаров (рабочих камер двигателей), а также с его течением по трубопроводам через местные сопротивления. Вследствие сжимаемости воздуха эти расчеты значительно сложнее, чем расчеты гидравлических систем, и в полной мере выполняются только для особо ответственных случаев. Полное описание процессов течения воздуха можно найти в специальных курсах газодинамики. Основные закономерности течения воздуха (газа) такие же, как и для жидкостей, т.е. имеют место ламинарный и турбулентный режимы течения, установившийся и неустановившийся характер течения, равномерное и неравномерное течение из-за переменного сечения трубопровода и все остальные кинематические и динамические характеристики потоков. Вследствие низкой вязкости воздуха и относительно больших скоростей режим течения в большинстве случаев турбулентный. Для промышленных пневмоприводов достаточно знать закономерности установившегося характера течения воздуха. В зависимости от интенсивности теплообмена с окружающей средой расчеты параметров воздуха выполняются с учетом вида термодинамического процесса, который может быть от изотермического (с полным теплообменом и выполнением условия Т = const) до адиабатического (без теплообмена). При больших скоростях исполнительных механизмов и течении газа через сопротивления процесс сжатия считается адиабатическим с показателем адиабаты k = 1,4. В практических расчетах показатель адиабаты заменяют на показатель политропы (обычно принимают n = 1,3…1,35), что позволяет учесть потери, обусловленные трением воздуха, и возможный теплообмен. В реальных условиях неизбежно происходит некоторый теплообмен между воздухом и деталями системы и имеет место так называемое политропное изменение состояния воздуха. Весь диапазон реальных процессов описывается уравнениями этого состояния pVn = const где n - показатель политропы, изменяющийся в пределах от n = 1 (изотермический процесс) до n = 1,4 (адиабатический процесс). В основу расчетов течения воздуха положено известное уравнение Бернулли движения идеального газа
Слагаемые уравнения выражаются в единицах давления, поэтому их часто называют "давлениями": На практике часто весовым давлением пренебрегают и уравнение Бернулли принимает следующий вид
Сумму статического и динамического давлений называют полным давлением P0. Таким образом, получим
При расчете газовых систем необходимо иметь в виду два принципиальных отличия от расчета гидросистем. Первое отличие заключается в том, что определяется не объемный расход воздуха, а массовый. Это позволяет унифицировать и сравнивать параметры различных элементов пневмосистем по стандартному воздуху (ρ = 1,25 кг/ м3, υ = 14,9 м2/с при p = 101,3 кПа и t = 20°C). В этом случае уравнение расходов записывается в виде Qм1 = Qм2 или υ1 V1S1 = υ2 V2S2 Второе отличие заключается в том, что при сверхзвуковых скоростях течения воздуха изменяется характер зависимости расхода от перепада давлений на сопротивлении. В связи с этим существуют понятия подкритического и надкритического режимов течения воздуха. Смысл этих терминов поясняется ниже. Рассмотри истечение газа из резервуара через небольшое отверстие при поддержании в резервуаре постоянного давления (рис.11.1). Будем считать, что размеры резервуара настолько велики по сравнению с размерами выходного отверстия, что можно полностью пренебрегать скоростью движения газа внутри резервуара, и, следовательно, давление, температура и плотность газа внутри резервуара будут иметь значения p0, ρ 0 и T0.
Рис.11.1. Истечение газа из отверстия в тонкой стенке Скорость истечения газа можно определять по формуле для истечения несжимаемой жидкости, т.е.
Массовый расход газа, вытекающего через отверстие, определяем по формуле
где ω0 - площадь сечения отверстия. Отношение p/p0 называется степенью расширения газа. Анализ формулы (11.7) показывает, что выражение, стоящее под корнем в квадратных скобках, обращается в ноль при p/p0 = 1 и p/ p0 = 0. Это означает, что при некотором значении отношения давлений массовый расход достигает максимума Qmax. График зависимости массового расхода газа от отношения давлений p/p0 показан на рис.11.2.
Рис.11.2. Зависимость массового расхода газа от отношения давлений Отношение давлений p/p0, при котором массовый расход достигает максимального значения, называется критическим. Можно показать, что критическое отношение давлений равно
Как видно из графика, показанного на рис.11.2, при уменьшении p/p0 по сравнению с критическим расход должен уменьшаться (пунктирная линия) и при p/p0 = 0 значение расхода должно быть равно нулю (Qm = 0). Однако в действительности это не происходит. В действительности при заданных параметрах p0, ρ 0 и T0 расход и скорость истечения будут расти с уменьшением давления вне резервуара p до тех пор, пока это давление меньше критического. При достижении давлением p критического значения расход становится максимальным, а скорость истечения достигает критического значения, равного местной скорости звука. Критическая скорость определяется известной формулой
После того, как на выходе из отверстия скорость достигла скорости звука, дальнейшее уменьшение противодавления p не может привести к увеличению скорости истечения, так как, согласно теории распространения малых возмущений, внутренний объем резервуара станет недоступен для внешних возмущений: он будет "заперт" потоком со звуковой скоростью. Все внешние малые возмущения не могут проникнуть в резервуар, так как им будет препятствовать поток, имеющий ту же скорость, что и скорость распространения возмущений. При этом расход не будет меняться, оставаясь максимальным, а кривая расхода примет вид горизонтальной линии. Таким образом, существует две зоны (области) течения: подкритический режим, при котором
надкритический режим, при котором
В надкритической зоне имеет место максимальная скорость и расход, соответствующие критическому расширению газа. Исходя из этого при определении расходов воздуха предварительно определяют по перепаду давления режим истечения (зону), а затем расход. Потери на трение воздуха учитывают коэффициентом расхода μ, который с достаточной точностью можно вычислить по формулам для несжимаемой жидкости (μ = 0,1...0,6). Окончательно скорость и максимальный массовый расход в подкритической зоне, с учетом сжатия струи определятся по формулам
|

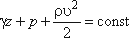
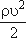 - скоростное или динамическое давление.
- скоростное или динамическое давление.