Решение. 1) Выпишем матрицу системы и найдем ее определитель (например, по правилу треугольников):
Пример решения типовой расчета
1) Выпишем матрицу системы и найдем ее определитель (например, по правилу треугольников):
Теперь найдем вспомогательные определители Получим:
Применяя формулы Крамера, найдем решение системы:
Сделаем проверку (самостоятельно!) и убедимся, что найденные значения неизвестных действительно являются решением исходной системы. 2) Матричный метод решения системы основывается на формуле:
Матрица
Проверьте самостоятельно, что обратная матрица найдена верно! Тогда 3) Метод Гаусса состоит в последовательном исключении неизвестных. Составим расширенную матрицу, приписав справа к матрице системы столбец свободных членов. Преобразуем полученную матрицу с помощью элементарных преобразований и приведем её к трапециевидной форме («прямой ход Гаусса»). Заметим, что при решении систем, преобразуют только строки матрицы!
Получим систему, равносильную исходной: Прочитав её снизу вверх («обратный ход Гаусса»), получим:
Ответ: Задание №3. Найти ранг матрицы
|
, заменяя в исходной матрице 
-ый столбец на столбец свободных членов (
т.е. 
.
, где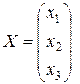 
– столбец неизвестных, 
– обратная матрица системы, 
– столбец свободных членов.
– неособенная (
), следовательно, она имеет обратную. Найдем 
.
. Следовательно, 
.
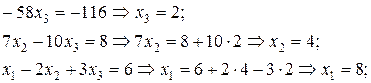
