1) Используем уравнение прямой в пространстве через две точки:

Подставляя координаты точек  , получим:
, получим:
 – уравнение ребра
– уравнение ребра  .
.
Длина стороны  равна длине вектора
равна длине вектора  .
.
 ед.
ед.
2) Площадь грани 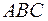 равна площади
равна площади  , которую можно найти через векторное произведение по формуле:
, которую можно найти через векторное произведение по формуле: 
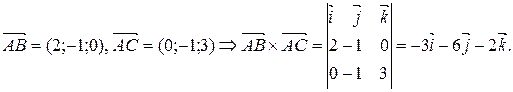
 кв. ед.
кв. ед.
Уравнение грани – это уравнение плоскости через три точки:

Подставляя в это уравнение координаты точек  , получим уравнение грани
, получим уравнение грани 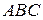 :
:

3) Объем пирамиды  равен
равен  модуля смешанного произведения векторов
модуля смешанного произведения векторов  . Найдем координаты векторов:
. Найдем координаты векторов:

Тогда смешанное произведение равно:

 куб. ед.
куб. ед.
4) Из уравнения грани 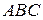 :
:  найдем координаты вектора нормали
найдем координаты вектора нормали  , расположенного перпендикулярно плоскости
, расположенного перпендикулярно плоскости 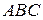 , а значит параллельно высоте, опущенной из вершины
, а значит параллельно высоте, опущенной из вершины  .
.
Используем каноническое уравнение прямой в пространстве:

Подставляя вместо  координаты точки
координаты точки 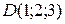 , а вместо
, а вместо 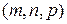 координаты вектора нормали
координаты вектора нормали  , получим уравнение высоты:
, получим уравнение высоты: 
Длина высоты  – расстояние от точки
– расстояние от точки  до плоскости
до плоскости 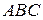 . Используем формулу
. Используем формулу 
Получим:  ед.
ед.
5) Угол  между ребром
между ребром  и гранью
и гранью 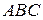 найдем как угол между векторами
найдем как угол между векторами  .
.
Имеем: 
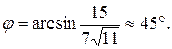
Заметим, что угол  по определению всегда острый. Поэтому, если
по определению всегда острый. Поэтому, если 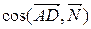 окажется меньше нуля, то его значение надо взять по модулю!
окажется меньше нуля, то его значение надо взять по модулю!
6) Угол  между гранями
между гранями 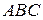 и
и  найдем как угол между нормалями к этим граням. Плоскость
найдем как угол между нормалями к этим граням. Плоскость 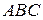 имеет уравнение
имеет уравнение  и, следовательно, её нормаль
и, следовательно, её нормаль  . Напишем уравнение плоскости
. Напишем уравнение плоскости  :
:

Тогда её нормаль  . Находим косинус угла между векторами
. Находим косинус угла между векторами  и
и  :
:

Замечание. Угол  по определению всегда острый. Поэтому, если косинус окажется меньше нуля, то его значение надо взять по модулю!
по определению всегда острый. Поэтому, если косинус окажется меньше нуля, то его значение надо взять по модулю!
Ответ:1)  ед.;
ед.;
2)  :
:  ;
;  кв. ед.;
кв. ед.;
3)  куб. ед.;
куб. ед.;
4)  – уравнение высоты; длина высоты
– уравнение высоты; длина высоты 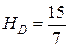 ед.;
ед.;
5)  6)
6) 


 , получим:
, получим: – уравнение ребра
– уравнение ребра  .
. .
. ед.
ед.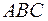 равна площади
равна площади  , которую можно найти через векторное произведение по формуле:
, которую можно найти через векторное произведение по формуле: 
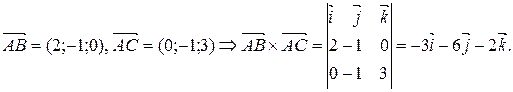
 кв. ед.
кв. ед.
 , получим уравнение грани
, получим уравнение грани 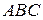 :
:
 равен
равен  модуля смешанного произведения векторов
модуля смешанного произведения векторов  . Найдем координаты векторов:
. Найдем координаты векторов:

 куб. ед.
куб. ед. найдем координаты вектора нормали
найдем координаты вектора нормали  , расположенного перпендикулярно плоскости
, расположенного перпендикулярно плоскости  .
.
 координаты точки
координаты точки 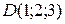 , а вместо
, а вместо 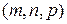 координаты вектора нормали
координаты вектора нормали 
 – расстояние от точки
– расстояние от точки 
 ед.
ед. между ребром
между ребром  .
.
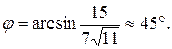
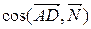 окажется меньше нуля, то его значение надо взять по модулю!
окажется меньше нуля, то его значение надо взять по модулю! между гранями
между гранями  найдем как угол между нормалями к этим граням. Плоскость
найдем как угол между нормалями к этим граням. Плоскость 
 . Находим косинус угла между векторами
. Находим косинус угла между векторами 
 ед.;
ед.; :
:  ;
;  кв. ед.;
кв. ед.; куб. ед.;
куб. ед.; – уравнение высоты; длина высоты
– уравнение высоты; длина высоты 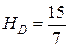 ед.;
ед.; 6)
6) 



