Endfunction

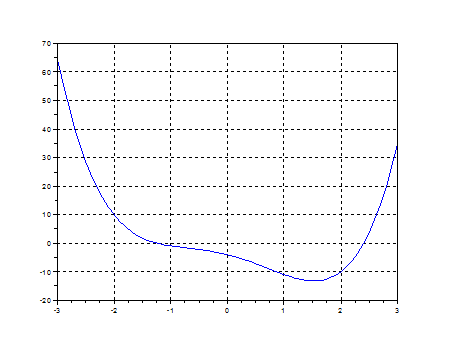
Если возвращаемое сформированной функцией costf значение ind равно 2, 3 или 4, то функция costf обеспечивает поиск минимума, т.е. в качестве результата функции optim возвращается f и xopt. Если ind=1, то в функции optim ничего не считается, условие ind<0 означает, что минимум f(x) не может быть оценен, а ind=0 прерывает оптимизацию. Вообще говоря, значение параметра ind является внутренним параметром для связи между optim и costf, для использования optim необходимо помнить, что параметр ind должен быть определен в функции costf.

Пример: найти минимум функции .

Решение. Построим график функции для определения интервалов [ a, b], на которых находятся экстремумы этой функции.

-->x=-3:.1:3; y=x.^4-3*x.^2-5*x-4; plot(x, y); xgrid()

Из графика видно, что это отрезок [1, 2]. Набираем в окне редактора и отправляем на выполнение файл

function [f,g,r]=z(x,r)

f=x.^4-3*x.^2-5*x-4

g=4*x.^3-6*x-5

endfunction

x0=1;

[fmin,xmin]=optim(z,x0)

Получаем

--> xmin =

1.5233402

fmin =

- 13.193373

Возможен другой вариант, без ручного вычисления производной:

function y=gg(x)

y=x.^4-3*x.^2-5*x-4;

endfunction

function [f,g,r]=z(x,r)

f=gg(x)

g=numdiff(gg,x)

endfunction

x0=1;

[fmin,xmin]=optim(z,x0)

 

xmin =

1.5233402

fmin =

- 13.193373

В случае функции двух переменных:

(Поиск минимума функции Розенброка )

clc

x0=[-2;2];

function y=gg(x)

y=100*(x(2)-x(1)^2)^2+(1-x(1))^2;

endfunction

function [f,g,r]=z(x,r)

f=gg(x)

g=numdiff(gg,x)

endfunction

[fmin,xmin]=optim(z,x0)

xmin =

0.9999955

0.9999910

fmin =

2.010D-11
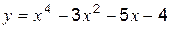
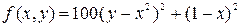