Плоское напряженное состояние
1. Арсеньев Б.П., Яковлев С.А. Интеграция распределенных баз данных. - СПб.: Лань, 2001. - 461с. 2. Бураков П.В., Петров В.Ю. Введение в системы баз данных: Учебное пособие. - СПб: СПбГУ ИТМО, 2010. - 128 с. 3. Голицина О.Л., Максимов Н.В., Попов И.И. Базы данных: Учебное пособие. - 2-е изд., испр. и доп. – М.: Форум, Инфра-М, 2009. - 400 с. 4. Горев А., Макашарипов С., Ахаян Р. Эффективная работа с СУБД. – М.: Финансы и статистика, 2004. – 298 с. 5. Дейт, К.Дж. Введение в системы баз данных. - 8-е изд., Пер. с англ. — М.: Вильяме, 2005. - 1328 с. 6. Диго, С. М. Базы данных: проектирование и использование: учебник для студ. вузов / С. М. Диго. – М.: Финансы и статистика, 2005. 592 с. 7. Кагаловский, М.Р. Энциклопедия технологий баз данных. – М.: Финансы и статистика, 2002. - 800 с. 8. Карпова, Т.С. Базы данных: Модели, разработка, реализация: Учебное пособие. - СПб.: Питер, 2002. - 303 с. 9. Коннолли, Т., Карелин Б. Базы данных. Проектирование, реализация и сопровождение. Теория и практика. 3-е изд.:пер. с англ. М.: Вильяме, 2003. - 1440 с. 10. Корнеев В.В., Гареев А.Ф., Васютин С.В., Райх В.В. Базы данных. Интеллектуальная обработка информации. - М.:Нолидж, 2000. - 352 с. 11. Корнеев И.К., Машурцев В.А. Информационные технологии в управлении. — М.: ИНФРА-М, 2001. - 158 с. 12. Коровин, Е.Н. Методология прогнозирования и оптимального управления территориально распределенными социально-экономическими системами на основе трансформации информации и многовариантного моделирования: Дис.... д-ра техн. наук. Воронеж, 2005. - 356 с. 13. Кузнецов С.Д. Основы баз данных. 2-е изд. М.: Бином, 2007. - 488 c. 14. Кульба В.В., Ковалевский С.С., Косяченко С.А., Сиротюк В.О. Теоретические основы проектирования оптимальных структур распределенных баз данных. – М.:СИНТЕГ, 1999 - 660с. 15. Макаров, C.B. Методы управления обновлениями и обеспечения согласованности информации в базах данных в расширенной архитектуре «клиент-сервер». Москва, 2000. - 145с. 16. Пушников А.Ю. Введение в системы управления базами данных. Часть 2. Нормальные формы отношений и транзакции: Учебное пособие/Изд-е Башкирского ун-та. - Уфа, 1999. - 138 с. 17. Пушников, А.Ю. Введение в системы управления базами данных. Часть 1. Реляционная модель данных: Учебное пособие/Изд-е Башкирского ун-та. - Уфа, 1999. - 108 с 18. Роб П., Коронел К. Системы баз данных: проектирование, реализация и управление. - 5-е изд., перераб. и доп. - СПб.: БХВ-Петербург, 2004. - 1040 с. 19. Таненбаум Э., Ван Стеен М. Распределенные системы. Принципы и парадигмы. СПб.: Питер, 2008 - 845с. 20. Таненбаум Э., Ван Стеен М. Распределенные системы. Принципы и парадигмы. - СПб: Питер, 2003. - 877с. 21. Ульман Д.Д. Введение в системы баз данных. М.: Лори, 2000. - 374с. 22. Цимбал А.А., Аншина М.Л. Технологии создания распределенных систем. Для профессионалов. - СПб.: Питер, 2003.-576 с.
7 c 58 Таненбаум Э., Ван Стеен М. Распределенные системы. Принципы и парадигмы. СПб.: Питер, 2008 - 845с.
Среди множества площадок, проходящих через точку тела, всегда можно провести три взаимно перпендикулярные площадки, касательные напряжения на которых будут равны нулю. Площадки, на которых касательные напряжения отсутствуют, называются главными, а действующие на этих площадках нормальные напряжения ¾ главными нормальными напряжениями. Направления нормалей к этим площадкам называются главными направлениями или главными осями. Докажем существование главных площадок и их ортогональность. Пусть наклонная площадка является главной. При этом полное напряжение
где l, m, n — направляющие косинусы нормали к площадке. Подставляя (4.14) в (4.9) и проводя преобразования, получаем
Основными неизвестными в системе линейных, однородных алгебраических уравнений (4.15) являются направляющие косинусы l, m, n; они не могут быть одновременно равны нулю, так как связаны соотношением (4.5). Поэтому для существования ненулевых решений определитель системы (4.15) должен быть равен нулю
Раскрывая определитель (4.16), приходим к кубическому уравнению относительно главного напряжения
где
Уравнение (4.17) называется характеристическим уравнением напряженного состояния. Коэффициенты Каждому значению главного напряжения Таким образом, в самом общем случае вектор полного напряжения pν в рассматриваемой точке тела может занимать произвольное положение, а геометрическое место концов вектора в пространстве образует эллипсоид напряжений (рис. 4.5), полуосями которого являются главные напряжения Из данного геометрического образа вытекает следствие, что наибольшее из трех главных напряжений является одновременно наибольшим из возможных полных напряжений pν на множестве площадок, проходящих через заданную точку тела. В случае равенства двух главных напряжений эллипсоид приобретает форму тела вращения, тогда каждая плоскость, проходящая через ось вращения, становится главной. Если же равны все три главных напряжения, то эллипсоид трансформируется в сферу и в исследуемой точке все секущие плоскости являются главными.
Рис. 4.5. Эллипсоид напряжений
Плоское напряженное состояние В случае плоского напряженного состояния
корни которого определяются равенствами
В случае линейного напряженного состояния два главных напряжения будут равны нулю, т. е. в уравнении (4.14) коэффициенты Главные напряжения обладают важным свойством: нормальные напряжения Теперь докажем ортогональность главных площадок. Сначала это сделаем для первой и второй главных площадок. Пусть направляющие косинусы первой главной площадки будут
Далее поступим следующим образом. Умножим уравнения (4.21) первой группы
Из анализа уравнения (4.22) видно, что при
Последнее равенство и есть условие ортогональности первой и второй главных площадок. Аналогично доказывается ортогональность других главных площадок. Напряжения на косых площадках при плоском напряженном состоянии Рассмотрим напряженное состояние пластинки толщиной Пусть заданы напряжения на площадках В случае плоского напряженного состояния тензор напряжений примет вид
Рис. 4.6. К определению напряжений на косых площадках
Величины
Если аналогично вычислить напряжения на площадке, нормаль к которой r перпендикулярна вектору нормали
Полученные формулы позволяют выявить важные закономерности. Так, складывая (4.23) и (4.25), имеем
Видно, что сумма нормальных напряжений на произвольных взаимно перпендикулярных площадках при их повороте не меняется. Сопоставляя (4.24) и (4.26), видим
т. е. касательные напряжения, действующие на произвольных взаимно перпендикулярных площадках, подчиняются закону парности. Положение главных площадок (касательные напряжения равны нулю) можно найти из (4.24) или (4.26), полагая
где Можно показать, что при заданных значениях
Обратная задача - если известны главные напряжения
|

 на площадке совпадет с нормальным напряжением
на площадке совпадет с нормальным напряжением  , а касательное напряжение
, а касательное напряжение  . Проекции полного напряжения
. Проекции полного напряжения  ,
,  ,
,  , (4.14)
, (4.14)
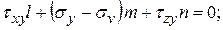 (4.15)
(4.15)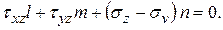
 . (4.16)
. (4.16) , (4.17)
, (4.17) ,
, (4.18)
(4.18) .
. называются инвариантами тензора напряжений, т. е. не зависящими от выбора системы координат. Решение кубического уравнения (4.17) в общем случае имеет три вещественных корня
называются инвариантами тензора напряжений, т. е. не зависящими от выбора системы координат. Решение кубического уравнения (4.17) в общем случае имеет три вещественных корня  , при них (как указывалось ранее) индексы надо расставлять так, чтобы выполнялось неравенство:
, при них (как указывалось ранее) индексы надо расставлять так, чтобы выполнялось неравенство:  . Понимать это равенство надо в алгебраическом смысле.
. Понимать это равенство надо в алгебраическом смысле. соответствует вектор нормали
соответствует вектор нормали 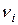 , характеризующий положение i -ой главной площадки с направляющими косинусами
, характеризующий положение i -ой главной площадки с направляющими косинусами  . Эти компоненты находятся подстановкой найденного значения
. Эти компоненты находятся подстановкой найденного значения 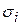 в любые два уравнения системы (4.15) и дальнейшим их решением совместно с условием нормировки
в любые два уравнения системы (4.15) и дальнейшим их решением совместно с условием нормировки  .
.

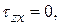
 равными нулю будут также коэффициент
равными нулю будут также коэффициент  и один из корней характеристического уравнения (4.17), то есть одно из главных напряжений обращается в нуль. При этом уравнение (4.17) перейдет в следующее
и один из корней характеристического уравнения (4.17), то есть одно из главных напряжений обращается в нуль. При этом уравнение (4.17) перейдет в следующее , (4.19)
, (4.19)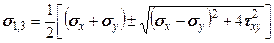 . (4.20)
. (4.20) .
.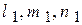 , а второй -
, а второй -  . Выпишем уравнения (4.15) для первой и второй главных площадок в виде
. Выпишем уравнения (4.15) для первой и второй главных площадок в виде
 (4.21)
(4.21)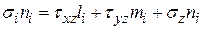 ,
, 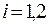 .
.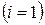 соответственно на
соответственно на  , а уравнения второй группы
, а уравнения второй группы 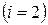 - на
- на  , а затем сложим все уравнения первой группы и отдельно второй. Вычитая из первой суммы вторую, получаем
, а затем сложим все уравнения первой группы и отдельно второй. Вычитая из первой суммы вторую, получаем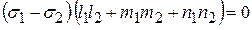 . (4.22)
. (4.22)
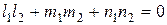 .
. , находящейся под действием сил Р, лежащих в плоскости пластинки (рис. 4.6). Будем считать, что под действием внешних сил пластинка находится в плоском напряженном состоянии, значит
, находящейся под действием сил Р, лежащих в плоскости пластинки (рис. 4.6). Будем считать, что под действием внешних сил пластинка находится в плоском напряженном состоянии, значит  . В выделенном элементе пластинки напряжения
. В выделенном элементе пластинки напряжения  ,
,  и
и 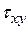 лежат в одной плоскости, поэтому напряженное состояние и называется плоским.
лежат в одной плоскости, поэтому напряженное состояние и называется плоским. и
и  элемента ABC. Надо определить нормальные напряжения
элемента ABC. Надо определить нормальные напряжения  на площадке BC, нормаль к которой
на площадке BC, нормаль к которой  составляет угол
составляет угол  с осью x. Массовыми силами, действующими на элемент ABC, пренебрегаем.
с осью x. Массовыми силами, действующими на элемент ABC, пренебрегаем. .
.
 определим из условия равновесия элемента ABC, составив соответствующие уравнения в проекциях на оси
определим из условия равновесия элемента ABC, составив соответствующие уравнения в проекциях на оси  и
и  . Опуская промежуточные математические выкладки, окончательно получим
. Опуская промежуточные математические выкладки, окончательно получим , (4.23)
, (4.23)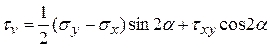 . (4.24)
. (4.24) , (4.25)
, (4.25) . (4.26)
. (4.26)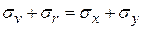 . (4.27)
. (4.27) , (4.28)
, (4.28)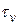 или
или  , следовательно
, следовательно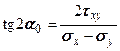 , (4.29)
, (4.29) — угол, который составляет нормаль
— угол, который составляет нормаль  главной площадки с осью
главной площадки с осью  .
. . (4.30)
. (4.30)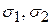 , то формулы для определения напряжений на наклонных площадках примут вид
, то формулы для определения напряжений на наклонных площадках примут вид ,
, , (4.31)
, (4.31) .
.


