Критерии (теории) прочности и пластичности
Вариант разделения по блокам
БЛОК – II БЛОК – III
Критерии (теории) прочности и пластичности 1. Критерий наибольших нормальных напряжений (первая теория прочности) (Галилей). Согласно этому критерию разрушение материала произойдет при достижении максимальным нормальным напряжением предельного (опасного) значения
Рис. 6.2. Критерий наибольших нормальных напряжений
Пригоден данный критерий для весьма хрупких материалов (камень, кирпич, керамика, инструментальная сталь). Особенность хрупких материалов является то, что они обладают различной сопротивляемостью при растяжении и сжатии, т. е. хрупкие материалы лучше работают на сжатие, чем на растяжение. В силу экстремальности главных напряжений в качестве максимального нормального напряжения выступает главное напряжение. По этому критерию
Максимальные напряжения при растяжении Известное условие прочности растяжение - где 2. Критерий наибольших линейных деформаций (вторая теория прочности) (Мариотт). Согласно этой теории в качестве критерия прочности принимают наибольшую по абсолютной величине линейную деформацию (рис. 6.3). Условие разрушения
Из обобщенного закона Гука имеем
При простом растяжении
Приравнивая формулы (6.2) и (6.3), имеем
Рис. 6.3. Критерий наибольших линейных деформаций
Критерий наибольших линейных деформаций дает удовлетворительные результаты для хрупких материалов, работающих в пределах закона Гука. Недостатком первых двух критериев прочности является тот факт, что они не описывают разрушение за счет сдвига, а только учитывают достижение опасного состояния за счет отрыва. 3. Критерий наибольших касательных напряжений (третья теория прочности) (Треск – Сен-Венан). Здесь в качестве критерия прочности принята величина наибольшего касательного напряжения. Условие разрушения имеет вид:
Рис. 6.4. Критерий максимальных касательных напряжений
Условие прочности по критерию максимальных касательных напряжений запишем в виде:
При сложном напряженном состоянии (как было показано выше)
При простом растяжении мы имеем
Приравнивая формулы (6.5) и (6.6), имеем
Основной недостаток данного критерия прочности - не учитывается влияние нормального напряжения 4. Критерий удельной потенциальной энергии формоизменения (четвертая теория прочности) (Губер). Согласно этой теории (рис. 6.5) опасное состояние (текучесть) в общем случае напряженного состояния наступает тогда, когда удельная потенциальная энергия формоизменения
Рис. 6.5. Критерий удельной потенциальной энергии формоизменения
Условие прочности в данном случае имеет вид
где Из предыдущей лекции известно (5.36), что удельная потенциальная энергия формоизменения
С другой стороны в эквивалентном одноосном напряженном состоянии
В соответствии с энергетическим критерием условие равноопасности элемента, находящегося в условиях сложного нагружения, и образца при простом растяжении запишется так
Тогда условие прочности по данному критерию примет вид
Критерий удельной потенциальной энергии формоизменения используется для пластических материалов, одинаково работающих на растяжение и сжатие.
5. Теория Мора Согласно теории Мора, два напряженных состояния равноопасны, если для соответствующих двух главных напряжений (
Отсюда вытекает формула для эквивалентного напряжения по теории Мора
Здесь коэффициент k представляет собой отношение предельных напряжений при одноосном растяжении и при одноосном сжатии. Если принять, что коэффициенты запаса прочности по отношению к предельным напряжениям растяжения и сжатия одинаковы, то k можно определить из выражения:
Окончательно условие прочности по теории Мора запишется следующим образом
Теория прочности Мора позволяет установить сопротивление разрушению материалов, обладающих разными сопротивлениями растяжению и сжатию. Как видим, гипотеза Мора (как и критерий наибольших касательных напряжений) не учитывает влияния промежуточного главного напряжения σ2 – это несомненный ее недостаток. Опыты показывают, что достаточно точные результаты гипотеза Мора дает для напряженных состояний смешанного типа, то есть для тех случаев, когда σ1 и σ3 имеют разные знаки. Таким образом, для практических расчетов следует рекомендовать четвертую (или третью) теории прочности для материалов, одинаково сопротивляющихся растяжению и сжатию, и теорию Мора – для материалов, различно сопротивляющихся растяжению и сжатию, то есть для хрупких материалов (для них в настоящее время пока еще применяют и вторую теорию прочности).
|


 , характеризующего свойства материала и не зависящего от вида напряженного состояния (рис. 6.2).
, характеризующего свойства материала и не зависящего от вида напряженного состояния (рис. 6.2).
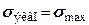 . (6.1)
. (6.1) ; при сжатии
; при сжатии  .
. запишем в виде:
запишем в виде: ; сжатие -
; сжатие -  ,
, ,
,  ,
,  — допускаемые напряжения соответственно при растяжении и сжатии, n — коэффициент запаса.
— допускаемые напряжения соответственно при растяжении и сжатии, n — коэффициент запаса. , где
, где  - опасная (предельная) продольная деформация. Условие прочности в этом случае имеет вид
- опасная (предельная) продольная деформация. Условие прочности в этом случае имеет вид .
. . (6.2)
. (6.2) . (6.3)
. (6.3) . (6.4)
. (6.4)
 , где
, где  — опасное (предельное) касательное напряжение (рис. 6.4).
— опасное (предельное) касательное напряжение (рис. 6.4).
 .
.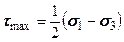 . (6.5)
. (6.5) . (6.6)
. (6.6) или
или  .
.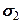 . Однако критерий наибольших касательных напряжений дает хорошие практические результаты при расчетах на прочность пластических материалов на начальном этапе пластических деформаций. Так как современные авиационные конструкции изготовлены в основном из пластических материалов и в процессе их эксплуатации недопустимы пластические деформации, то указанный критерий нашел широкое применение при расчетах на прочность именно авиационных конструкций.
. Однако критерий наибольших касательных напряжений дает хорошие практические результаты при расчетах на прочность пластических материалов на начальном этапе пластических деформаций. Так как современные авиационные конструкции изготовлены в основном из пластических материалов и в процессе их эксплуатации недопустимы пластические деформации, то указанный критерий нашел широкое применение при расчетах на прочность именно авиационных конструкций. достигает своего предельного значения
достигает своего предельного значения  .
.
 , (6.7)
, (6.7) — допускаемая удельная потенциальная энергия формоизменения.
— допускаемая удельная потенциальная энергия формоизменения. . (6.8)
. (6.8) энергия формоизменения будет равна
энергия формоизменения будет равна . (6.9)
. (6.9)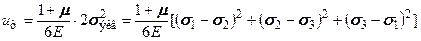 . (6.10)
. (6.10) . (6.11)
. (6.11) и
и  ) соблюдается соотношение
) соблюдается соотношение . (6.12)
. (6.12) . (6.13)
. (6.13)
 (6.14)
(6.14)


