Прайс-лист: Бизнес центр «Виктория», г. Курган, ул. Кравченко, 55.
При деформации тела его точки перемещаются, при этом изменяются расстояния между точками и углы между отрезками, соединяющими эти точки. Обозначим линейные перемещения точки вдоль осей соответственно Оx,Оy,Оz через u, v, w. На рис. 5.1 слева изображен прямоугольный параллелограмм, вырезанный вокруг некоторой точки тела с длинами сторон dx, dy, dz. После деформации длины его сторон изменятся:
Рис.5.1. К нахождению составляющих тензора деформации
Деформированное состояние в точке тела характеризуется совокупностью относительных линейных Покажем, как определяются компоненты относительных линейных и угловых деформаций на примере плоского случая деформирования элемента (рис. 5.2). Пусть плоский элемент ABCD под действием нагрузки перемещается (за счет общей деформации тела) в пределах плоскости и деформируется (изменяет размеры и форму), трансформируясь в элемент По определению относительная линейная деформация в точке A по направлению оси Ox равна
где элементарные длины отрезков
В случае малых деформаций
Подставляя (5.3) в (5.1), получаем
Рис. 5.2. К нахождению составляющих тензора деформации
Из рис. 5.2 видно, что угловая деформация
В случае малых деформаций и учитывая, что
С учетом (5.6) выражение (5.5) окончательно принимает форму
Обобщая аналогичные выкладки на общий случай трехмерной деформации, имеем
Соотношения (5.8) носят название соотношений Коши. Три линейных
Тензор (5.12) полностью определяет деформированное состояние твердого тела. Он обладает теми же свойствами, что и тензор напряжений, так как строится в рамках закона взаимно однозначного соответствия между напряжениями и деформациями, т. е. в рамках закона Гука.
5.2. Закон парности касательных напряжений при объемной деформации Не все девять компонентов напряжений, действующих на гранях элементарного параллелепипеда, являются независимыми. В этом легко можно убедиться, составив уравнения моментов для выделенного плоского элемента (рис. 5.3). Составим уравнение моментов относительно оси О z - точки
Рис. 5.3. К выводу закона парности касательных напряжений
Отсюда следует
Аналогично для 2-х других уравнений можем найти
Итак, равенства Он гласит: касательные напряжения на двух любых взаимно перпендикулярных площадках, направленные перпендикулярно к линии пересечения площадок, равны по величине и направлены либо оба к линии пересечения, либо от нее.
5.3. Обобщенный закон Гука для изотропных тел Для большинства конструкционных материалов свойство упругости проявляется при умеренных значениях внешних сил, приводящих к малым деформациям, и при малых скоростях нагружения, когда потери энергии за счет температурных эффектов пренебрежимо малы. Материал называется линейно-упругим, если компоненты тензора напряжений Одноосное напряженное состояние. Пусть материал является линейно-упругим и изотропным. Рассмотрим элементарный объем, находящийся в условиях одноосного напряженного состояния (рис. 5.4).
Рис. 5.4. Одноосное напряженное состояние Тензор напряжений в этом случае будет иметь вид
При таком нагружении направление действия напряжения будет характеризоваться линейной деформацией, пропорциональной величине напряжения
где Е — модуль упругости Соответствующие деформации по направлениям 2 и 3 обозначим через
где μ - коэффициент Пуассона.
Трехосное напряженное состояние. При одновременном действии напряжений по трем ортогональным осям (рис. 5.5), когда отсутствуют касательные напряжения, тензор напряжений будет
Рис. 5.16. Трехосное напряженное состояние. Главные площадки
Используя принцип суперпозиции, можно записать
С учетом формул типа (5.14), (5.15) зависимости (5.17) примут вид
Соотношения (5.18) справедливы для главных направлений (главных площадок). Доказано, что они справедливы для любых трех взаимно перпендикулярных направлений.
Это и понятно, так как при малых деформациях скос (сдвиг), вызываемый касательными напряжениями, не влияет на изменение длины отрезков. Поэтому зависимости (5.19) выражают так называемый обобщенный закон Гука. Связь между деформациями сдвига и касательными напряжениями. Угловая деформация (деформация сдвига) обусловлена касательным напряжением. Так, например, деформации Соответствующие касательные напряжения и угловые деформации для линейно-упругого изотропного тела связаны зависимостями
где G — модуль сдвига. Между E и G для изотропных материалов существует связь
Объемная деформация. Пусть параллелепипед со сторонами
Рис. 5.7. К определению объемной деформации
Объем параллелепипеда до деформации был
Последнее выражение представим в виде:
Относительное изменение объема при пренебрежении произведениями величин
С учетом (5.19) выражение (5.21) примет форму:
Для случая гидростатического сжатия:
Величина При Из опытов следует, что для всех известных материалов 5.4. Потенциальная энергия упругой деформации В общем случае нагружения тела по граням его элемента (параллелепипеда) с размерами ребер Рассмотрим вначале элементарный объем
При отсутствии потерь энергии при нагружении в силу закона сохранения энергии совершаемая работа перейдет в потенциальную энергию, накапливаемую в процессе деформирования тела
Рис. 5.8. К определению потенциальной энергии деформации
Удельная потенциальная энергия, накопленная в единице объема элемента, будет
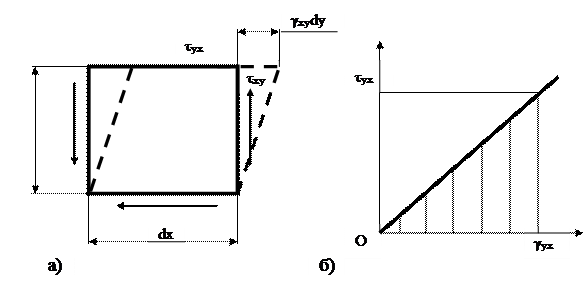
В частном случае чистого сдвига в плоскости Соответствующая этому случаю нагружения удельная потенциальная энергия деформации равна (рис. 5.9 б)
В общем случае напряженно-деформированного состояния будем иметь
Выражая деформации в (5.28) через напряжения с помощью обобщенного закона Гука (5.19), окончательно имеем
Рис. 5.9. К определению потенциальной энергии при сдвиге
или в главных напряжениях
Ранее было показано, что объемное напряженное состояние всегда можно представить как сумму напряженных состояний, одно из которых характеризует объемную деформацию элемента тела, а второе - изменение его формы. Удельную потенциальную энергию также можно представить в виде суммы
где Найдем сначала удельную потенциальную энергию изменения объема элемента
или
Удельную потенциальную энергию формоизменения
Заменяя в (5.34)
или
В случае всестороннего равномерного сжатия
Прайс-лист: Бизнес центр «Виктория», г. Курган, ул. Кравченко, 55. Многофункциональное административное здание с возможностью размещения офиса крупной компании.
|

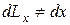 ,
, 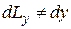 ,
, 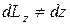 . Поменяются и углы между сторонами соединяющими, например, точки
. Поменяются и углы между сторонами соединяющими, например, точки 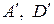 и
и  (рис. 5.1 справа); здесь
(рис. 5.1 справа); здесь 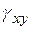 - угол сдвига.
- угол сдвига.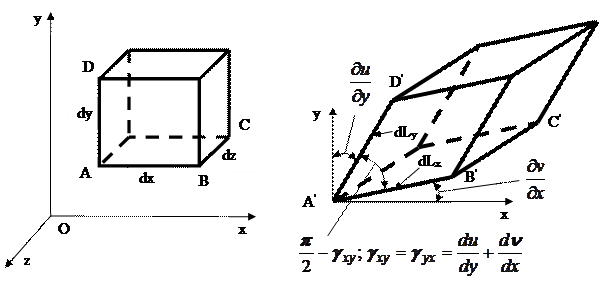
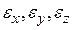 и угловых сдвиговых деформаций
и угловых сдвиговых деформаций 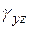 ,
, 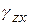 по всем декартовым направлениям Оx,Оy,Оz, проходящим через данную точку тела.
по всем декартовым направлениям Оx,Оy,Оz, проходящим через данную точку тела.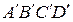 . Координаты точек элемента до и после его деформирования показаны на рис. 5.2.
. Координаты точек элемента до и после его деформирования показаны на рис. 5.2.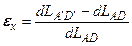 , (5.1)
, (5.1)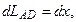 а
а 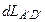 определяется по формуле
определяется по формуле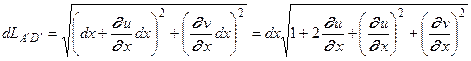 (5.2)
(5.2)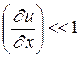 и
и 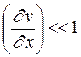 квадратными членами в (5.2) можно пренебречь. Раскладывая оставшуюся часть подкоренного выражения в биноминальный ряд и удерживая первые два члена, будем иметь
квадратными членами в (5.2) можно пренебречь. Раскладывая оставшуюся часть подкоренного выражения в биноминальный ряд и удерживая первые два члена, будем иметь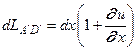 . (5.3)
. (5.3)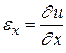 . (5.4)
. (5.4)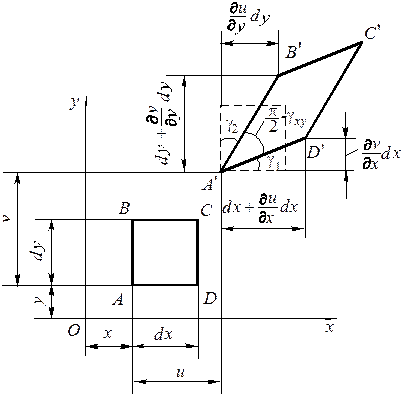
 равна
равна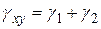 . (5.5)
. (5.5)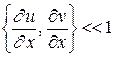 , имеем
, имеем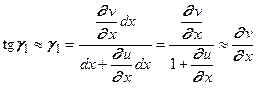 , (5.6)
, (5.6)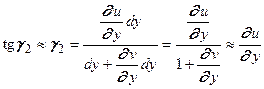 .
.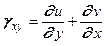 . (5.7)
. (5.7)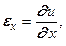

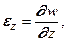 (5.8)
(5.8)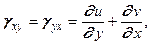
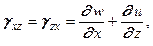
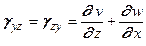 .
.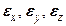 и шесть угловых
и шесть угловых 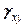 ,
, 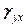 ,
, 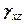 ,
, 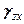 ,
, 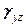 ,
, 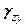 деформаций образуют тензор деформаций
деформаций образуют тензор деформаций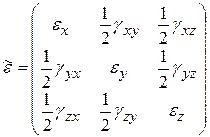 . (5.9)
. (5.9)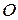 (рис. 5.3):
(рис. 5.3):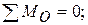 тогда
тогда 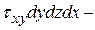
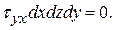 (5.10)
(5.10)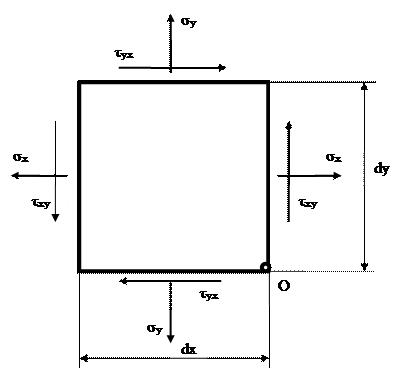
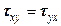 . (5.11)
. (5.11)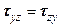 ;
; 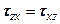 . (5.12)
. (5.12)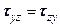 ;
; 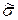 и тензора деформаций
и тензора деформаций 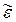 связаны линейными соотношениями.
связаны линейными соотношениями.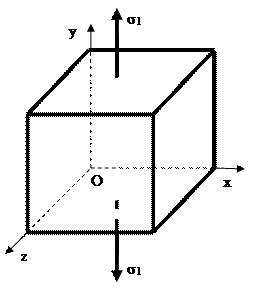
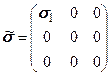 . (5.13)
. (5.13)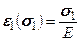 , (5.14)
, (5.14)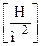 .
.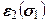 и
и 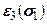 , причем они будут отрицательны при
, причем они будут отрицательны при 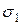 >0 и пропорциональны
>0 и пропорциональны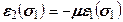 ,
, 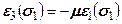 , (5.15)
, (5.15)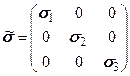 . (5.16)
. (5.16)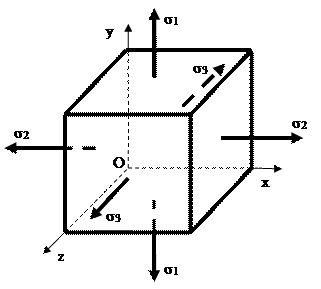
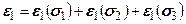 ,
,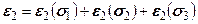 , (5.17)
, (5.17)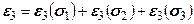 .
.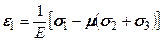 ,
,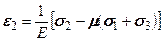 , (5.18)
, (5.18)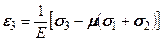 .
.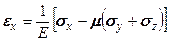 ,
, , (5.19)
, (5.19)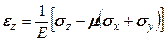 .
.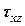 ,
, 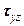 .
.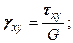
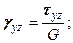
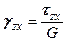
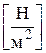 , (5.20)
, (5.20)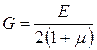 .
. (рис. 5.7 а) после нагружения изменил свои размеры (рис. 5.7 б).
(рис. 5.7 а) после нагружения изменил свои размеры (рис. 5.7 б).

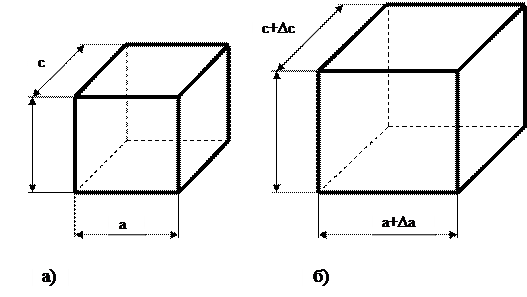
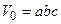 , а после деформирования составил:
, а после деформирования составил: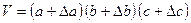 .
.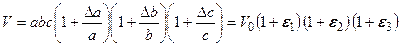 .
.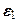 ,
, 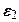 и т. д., как величинами второго порядка малости равно:
и т. д., как величинами второго порядка малости равно: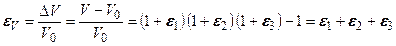 . (5.21)
. (5.21)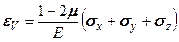 . (5.22)
. (5.22)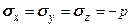 (p ¾ равномерное давление) соотношение (5.22) предстанет в виде
(p ¾ равномерное давление) соотношение (5.22) предстанет в виде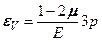 . (5.23)
. (5.23)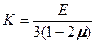 — называется модулем объемной деформации.
— называется модулем объемной деформации.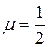 (предельное значение) изменения объема не происходит, это так называемые несжимаемые материалы.
(предельное значение) изменения объема не происходит, это так называемые несжимаемые материалы.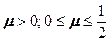 ; для конструкционных материалов
; для конструкционных материалов 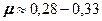 .
.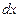 ,
, 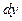 ,
, 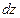 , вырезанного вокруг произвольной точки тела, будут действовать нормальные
, вырезанного вокруг произвольной точки тела, будут действовать нормальные 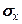 ,
, 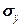 ,
, 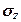 и касательные напряжения
и касательные напряжения 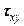 ,
, 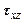 ,
, 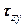 . Потенциальная энергия, накопленная в этом элементе при деформации тела, будет равна сумме работ внешних для выделенного элемента нормальных
. Потенциальная энергия, накопленная в этом элементе при деформации тела, будет равна сумме работ внешних для выделенного элемента нормальных 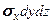 ,
, 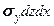 ,
, 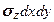 и касательных сил
и касательных сил 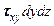 ,
, 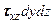 ,
, 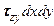 соответственно на удлинениях ребер параллелепипеда
соответственно на удлинениях ребер параллелепипеда 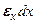 ,
, 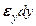 ,
, 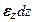 и перемещениях граней параллелепипеда
и перемещениях граней параллелепипеда 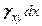 ,
, 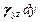 ,
,  .
.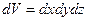 в условиях одноосного напряженного состояния (рис. 5.8 а). Сила
в условиях одноосного напряженного состояния (рис. 5.8 а). Сила 
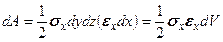 . (5.24)
. (5.24)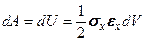 . (5.25)
. (5.25)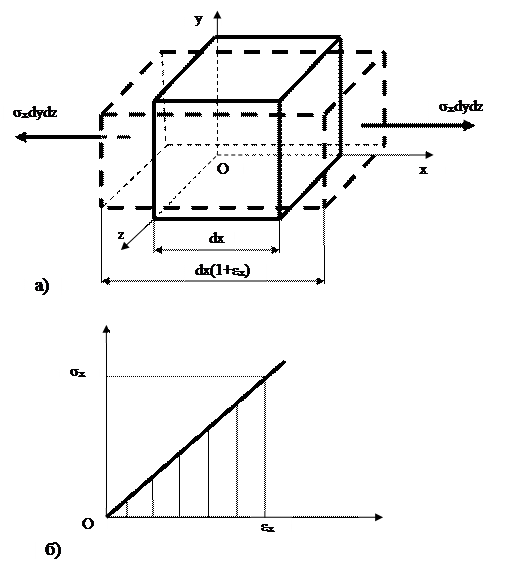
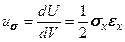 . (5.26)
. (5.26)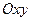 , изображенной на рис. 5.9 а, сила
, изображенной на рис. 5.9 а, сила  совершает работу на перемещении
совершает работу на перемещении 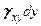 .
.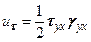 . (5.27)
. (5.27)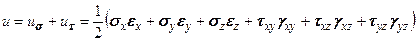 . (5.28)
. (5.28)
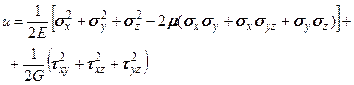 (5.29)
(5.29)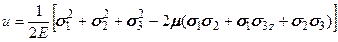 . (5.30)
. (5.30)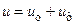 , (5.31)
, (5.31)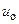 ,
, 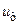 — части удельной потенциальной энергии
— части удельной потенциальной энергии 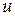 , пошедшие на изменение, соответственно, объема и формы выделенного элемента в окрестности исследуемой точки.
, пошедшие на изменение, соответственно, объема и формы выделенного элемента в окрестности исследуемой точки.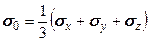 . Поэтому для определения
. Поэтому для определения 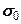 вместо
вместо 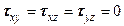 , тогда
, тогда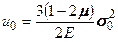 (5.32)
(5.32)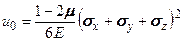 . (5.33)
. (5.33)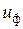 проще найти как разность
проще найти как разность 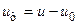 .
.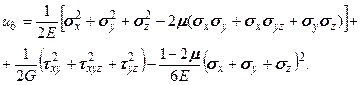 (5.34)
(5.34)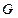 на
на 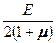 и проводя преобразования, получаем
и проводя преобразования, получаем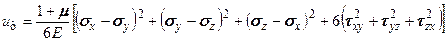 (5.35)
(5.35)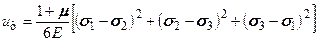 . (5.36)
. (5.36)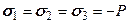 энергия формоизменения элемента
энергия формоизменения элемента 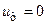 , то есть происходит изменение только объема элемента при неизменной его форме.
, то есть происходит изменение только объема элемента при неизменной его форме.


