Для полного исследования функции найдем первую и вторую производные:
Исследуемая функция:  Производные:
Производные:

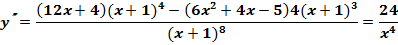
Таким образом: 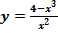 ,
, 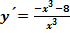 ,
, 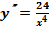
Найдем критические точки по определению:
Определение. КРИТИЧЕСКОЙ ТОЧКОЙ функции  называется внутренняя точка области определения, в которой производная называется внутренняя точка области определения, в которой производная 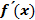 равна нулю или не существует. равна нулю или не существует.
|
В нашем случае производная не существует в точке  . Но эта точка является точкой разрыва и не входит в область определения, поэтому не является критической.
. Но эта точка является точкой разрыва и не входит в область определения, поэтому не является критической.
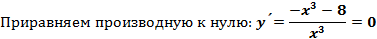
Отсюда 

ДОСТАТОЧНОЕ УСЛОВИЕ ВОЗРАСТАНИЯ, УБЫВАНИЯ ФУНКЦИИ:
Если на интервале производная 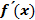 положительна, то функция положительна, то функция  возрастает, если отрицательна, то убывает. возрастает, если отрицательна, то убывает.
|
Знак производной может измениться только в критических точках или в точках разрыва функции.
Покажем знаки производной на числовой оси:
Функция возрастает на интервалах: 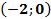 .
.
Функция убывает на интервалах:  .
.
ПЕРВОЕ ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА:
Пусть функция  непрерывна в точке непрерывна в точке 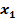 и дифференцируема в окрестности этой точки. Тогда, если при переходе через точку и дифференцируема в окрестности этой точки. Тогда, если при переходе через точку 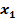 слева направо производная слева направо производная  меняет знак: 1) с + на -, то в точке меняет знак: 1) с + на -, то в точке 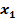 максимум; 2) с - на +, то в точке максимум; 2) с - на +, то в точке 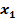 минимум. минимум.
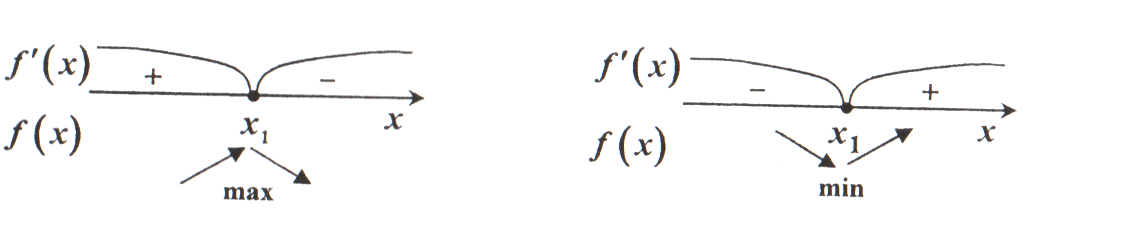 Если производная не меняет знак, то экстремума в этой критической точке нет.
Если производная не меняет знак, то экстремума в этой критической точке нет.
|
В нашем случае: 
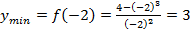 .
.

 Производные:
Производные:
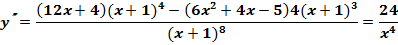
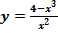 ,
, 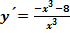 ,
, 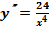
 называется внутренняя точка области определения, в которой производная
называется внутренняя точка области определения, в которой производная 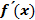 равна нулю или не существует.
равна нулю или не существует.
 . Но эта точка является точкой разрыва и не входит в область определения, поэтому не является критической.
. Но эта точка является точкой разрыва и не входит в область определения, поэтому не является критической.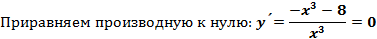


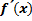
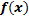
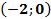 .
. .
. непрерывна в точке
непрерывна в точке 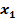 и дифференцируема в окрестности этой точки. Тогда, если при переходе через точку
и дифференцируема в окрестности этой точки. Тогда, если при переходе через точку  меняет знак: 1) с + на -, то в точке
меняет знак: 1) с + на -, то в точке 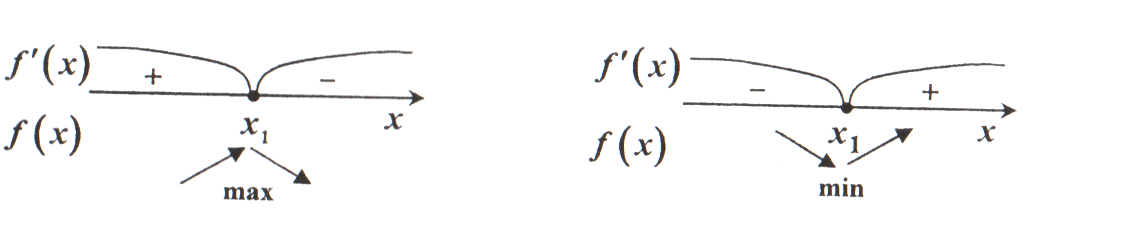 Если производная не меняет знак, то экстремума в этой критической точке нет.
Если производная не меняет знак, то экстремума в этой критической точке нет.

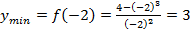 .
.


