Динамика-2.
Тема: Общие теоремы динамики..
35. Какой формулой описывается теорема о движении центра масс механической систе- 1.**»с=1^: 2.-V' : у.Щг-±5:. м йх '=1 ы\ 36. Могут ли внутренние силы изменить движение центра масс механической системы? 37. При каких условиях будет выполняться закон сохранения движения центра масс мех системы? 1.2 = 0; 2. = 0; 3. X = 0; 4. а = const. /=1 1=1 ' (=1 38. Если к неподвижному свободному твердому телу приложить пару 1. произвольно; 2. вокруг центра масс; 3. вокруг одной из точек приложения сил пары.
39. Однородный диск, радиус которого R=0,1m, масса т=5 кг вращается с угловым уско- рением Е — 2 ряд/ С вокруг оси. проходящей через его центр масс перпендикулярно плоскости диска. Определить модуль главного вектора внешних сил. действующих на диск. 40. Назовите меры механического движения твердого тела. 1. Момент инерции. 2. Количество движения. 3. Кинетическая энергия 4. Кинетический момент 41. Чему равно количество движения Q материальной точки? 1. g = mV; 2. CJ = fxV; 3. Ц-тй. 42. Какая формула описывает теорему об изменении количества движения Ц матери- *-.«-•> mr(b). о =q. з - У FI at щх dt dt 7~r 43. При прямолинейном движении точки массой m= 5 кг, при действии на нее системы сил, ее скорость изменилась с 4 м/с до 10 м/с. Определите в [Не] импульс равнодействующей сил за промежуток времени, в течение которого эти силы изменили скорость точки. 44. Что называется импульсом S переменной силы Р за конечный промежуток времени ее действия t? ,. г р. l.S = Pdt: 3.8 = о t 45. Чему равно изменение количества движения точки за некоторый промежуток време- 1. Равнодействующей сил, приложенных к точке 2. Импульсу равнодействующей 3. Моменту равнодействующей 46. По каким формулам можно найти главный вектор Q количеств движения механиче-
г =1 1 = 1 47. Какими формулами описывается теорема об изменении главного вектора количеств движения механической системы?
ы\ /=1 <#,=| J/ frf 48. Выбрать условия при которых выполняется закон сохранения главного вектора количеств движения механической системы. Ш'=°; 2.2>д^) = 0; 3.1^=0; 4.±т,(р;) = о. /=1 /=1 1=1,'=1 49. Могут ли внутренние силы изменить главный вектор количеств движения системы? 1. Не могут. 2. Могут при определенных условиях. 3. Могут. 50. По какой из формул можно найти момент относительно центра (т.О) количества движения точки? 1. то(ту) - V х р ; 2. т0(тЪ) = Г х гт>; 3. то{тл!) - р х ту. 51. Какая из формул описывает теорему об изменении момента количества движения х.Щ^=тлР), г «>ч)-*.<»*.)-*.(*): з. &№тЩЛт. 52. Известна зависимость от времени момента количества движения точки относительно оси Ъ т2(тУ) = Ш (где 1 - время в с). Определите при 1=2с момент относительно оси Ъ действующей на точку силы. 53. Если у вращающегося вокруг оси Ъ твердого тела увеличить кинетический момент 1. быстрее; 2. медленнее; 3. так же. 54. Что называется кинетическим моментом К0 механической системы относительно 1. Сумма кинетических энергий всех точек системы. 2. Сумма моментов количеств движения всех точек системы относительно данного центра. 3. Сумма моментов внешних сил относительно данного центра. 55. Чему равен кинетический момент Кг относительно оси Ъ твердого тела, вращающегося вокруг этой оси с угловой скоростью СО —2 рад/ с, если момент инерции его Л =0,3кгм2?: 56. Какое из уравнений выражает теорему об изменении кинетического момента механической системы? 57. При каких условиях выполняется закон сохранения кинетического момента системы? 1. Ър'=й;2.5>0(3*)=о; з.1^=о; 4.5>л^)=о. Н,=1 ы
58. Если у изменяемой механической системы, вращающейся вокруг оси Ъ, момент инерции «/г увеличить только за счет внутренних сил (внешние силы не действуют), то угловая скорость системы... 1. не изменится 2. увеличится 3. уменьшится 59. У движущейся материальной точки скорость увеличилась в 2 раза. 60. Укажите формулы, в которых элементарная работа силы F найдена правильно. \. dA = Fdtcosa; 2. dA - F1 • df; з. dA = F • dv ; A.dA- Fds cos a. 61. Если из начального положения под действием силы тяжести материальная точка 1. больше, чем в первом; 2. меньше, чем в первом; 3. такая же. как в первом. 62. Дано определение работ четырех сил. Какие из них откосятся к потенциальным? i.AVv/, = \f^ds; 2.AMo,lt=±Gh; з.//..,„„ = сЛ%-%); 4. Av/, = "'v 63. Какие формулы описывают теорему об изменении кинетической d !; dt { 2 ч\ mv J (2 \ mv V 2 j M ту,2 _ пм\ Л ту,2 _ ту2 А 2 з. _ 0 ^л'л/0а/,; 4- о о ^ ' ■ 4 £ м ^ ^ 1=1 64. Какому движению тела соответствует формула для определения его кинетической
1. Поступательное. А. /=■■---•, ;;Ч ■ : ■■ ■ ■•• ' 2
2. Вращательное. В. 1 — + ■ 2 2 _ тт>с 3. Плоскопараллельное. С. * — _ • 65. Определите работу пары сил, приложенной к вращающемуся вокруг оси Ъ телу, если (р — Ъ?Г (считать 71 ~ 3). 66. Назовите единицу измерения работы силы. 1. Вт. 2. Дж. З.Нс. 67. Укажите единицу измерения кинетической энергии. кг ■ м 1. Дж. 2..................... 3. кВт. с 68. По реке движется моторная лодка со скоростью 5 м/с, Сила тяги двигателя равна 10СО Н. Определите в кВт мощность этой силы. 69. Диск вращается под действием пары сил, момент которой относительно оси вращения Z - Мг =20 Нм. Определите мощность, которая необходима для придания диску угловой скорости СО = 0,4 рад/с. 70. Какие из приведённых формул описывают теорему об изменении кинетической эне)-гии механической системы?
;=| 1=1,=1,=|
■•-I I-I ■,=1
; рй Г ■■ Ь. x,,. = хя - О;. у0 * t[,a О", \/ох = Vg-cos&'t Voy =- /g-sinuc. изобразим брикет г произвольном лоложеаик -Z/v и укажем .: еиств.үющиө на нэго силы: отыестк Р_ направим вертииняьно -?нчэ,. ;' Р •= /V +/-0 лорэменную силу /• направим в г олокктольном направлении рек ¿5;•', так как *~х> О -
Составив ^Hqijеренцкальнке. уравне да:
(3.8.)
(3.9)
Учитывая, что ь н по оси by нет движения), получаем dt* n =- р. I Но = /Л/.значит, fp ~.
' По,а!получк!:
dt*
j erf После разделения переиәнных имеем: fr?oїy - н-simol di ~ fPdt. Проинтегрируем • mJdV = hjsL^cotat -JfPdt. фокчам: mV = „JL cos coty-^Pt-^Зf. (3.10)
Замеьив V на и разделив переменные. уравнению (3.10) придадим вид: ' " mdx -~ -~~ їos cot dt -fPt dt ■+ dt, Проинтегрируем Wo^- coscotdt-WPtdt ■*• [c.dt j -soi j j 7) найдем; x*------- * slncаt-falL +Jkt + C?. (у.11) Для определения подставим в сравнение (3.10) началь-ные условия (t -.0, = t&fiftSoO: /??к^о(- J±. ces, оо-О - /Р-О + С-,.
■ Для определения начальные условия (t к-о, ^0~^s - 0j подставик в уравнение (3.11):
§p;.$ї ■.■{-- ' г ■ После подстановки в уравнение (3.11) з.-ачекии С1 и. Г,, окончательно имееа: X г -.Л. ию tфt - її'-ї'Ь» tt?Xн/* t+^t f/7Cщs? 2 & miу или
Окончательно;
' 1
ч подставим (3.~) в лрьшые части уравнений:
Учитывая, что *Рл1пс(> * р-са&(£,. получим:
Так как брикет двигается вдоль оси с*,, то будем расаматри-: аать одно дифференциальное уравнение; * ^ЗтГ = А ^ (3.4) Заменим и урэвиеьли (3.4.} значение переменной силы 7? =хуиН
запишем его тал: /г? - • /?с< - /и И, или " от. _ ^ /''гдйюс \
Обозначив ^ ^^^^). Разделим переменные проинтегрируем и получим: _ -Ь^-У)*^ +С\, ' (3.5) Подставив в (3,5; начальные условия = 0 и \£ --- 0 Ь на- уравнение (3.5) после, подстановки в него значения С-1 принимает вид: т ~-------- £
~_ е * \
*/= <*(•/.- 6» у. (з.б) Подставив ч (З.б) время ^ движения брикета от точки А 10 тощ«и В, кайдем скорость брикета в точке В:
Поде-тешив численные значения величин, входящих э (3.7),. юпучим: 1^5 ><^10 м/с. Рассмотрим движение брикета:ш участке ВС. Выберем систему координат, как показано на рис. 3. Запишем начальные условия: *ї"<X -f'Co&dL)tc'.t + CTdj.. Проинтегрировав это выражение, получим: X ~%{пind - f-co^-f, C,t +Ce. ( 2.5, Шдетавиз в,равне:ие (2.41 t = о и V = О, нчходий! а* О, - подставив в уравнение (г.Ч),? г. О и Х0 = О, находим <v = ї?,' После подстановки значений їvи в уравнение (2.5), окончательно получим уравнение движения ичдтра- тяжести нока спрео-ооввышго сена:
Что>й» найти время движения, в ура;.-нении (2,.6) надо за-ме нить X fa rs. В результате г.зчены получим:
Откуда
£ =. П еле подстановки численных значений величин, входтщих г выражение (<Ў.7), получим, что £ - 2 2 с. ЗАДАЧА Л 3 Брикет биокорма -Z? массой.т, иолутв в точке Л иа-чалвную скорость V0, движется по изогнутому желобу ABC, расположенному в вертакнльной плоскости (jjhc. 3J. Угол наклона oн- = 30°. На учаеше АВ на брикет, кроме силы тяжести, дейст-
Рассмотрим движение брикета на участке №. Выберем систему координат..¥> {^«совместив начало отсчета ■О1 о начальным положением А брикета &. Ось направим вниз ;вдоль желоба, ось 0,Уг перпендикулярно к <2,Х/. Запишем* начальные условия.
Тек как движение брикета Х> началось из точки А, которую (3.1 } Изобразим брикет в произвольно*/ положении D-Ў к укажем действующие m него_еилн: сиг' тяжести Р направив ьерт5рсально вниз, силу сопротивления Я направим протк движении брикета, 10 м, если угол наклона плоскости к горкеой^ о<» у о" и коэффициент трения / = ОД. ем суммы прекций сил 1& оси координат: V р - Р - Р
Решение
Начальное положение /% центра тяжести тюка (рио. 2) причем за начало отсчета О, Ось ОХ направим ениз по наклонной плоскости, а ось ОУ проведем перш здикулярко к оси ОХ. или
Запишем начальные условия: 1) координаты точки /%; 2) проекции начальной скорости на оси координат. В задаче У0 = 0, п этому при = О *° - о, ^г. О. Кх*> о, о. Изобразим центр тяжести тюка I п^оивнсдьном положении в вице точки /V и нанесем действ,,,ощ1 е на точку силы: силу тяжести Р, направив вертикально вниз; реакцию связг; Я, учитывая, ! го
где /V - нормальная составляющая реакции связи, • /}р - сила трения, равная
Силу Р разложим на соо*ввл;йощн5 Р< и Щ, подсчита
точки: (■ал)
то Так как * 0 (движение только вдоль оси ОХ), 5 ив"уравнения (2.2)
Значит, //V = /Р< С^ос ; и урвенение ф-1) примет вид /"/7 или &У - П (£.1*?Ы (2.3) В уравнении (2.3) разделим переметив и, проинтегриро- вав
получим.
Заменив V - ~тг > запишем; Тогда диф£е}»**8йиьдае уравнение движений точки $Й»Й^Чиы в виде: Откуда
г <* :, уравнении < Я | сделкам замену: ч разделим Шфвмшш 7^0 = <*' ■ Проинтегрировать щш Шфйжвтв получим: -~&(9>-кУ)^ +С,. (з) Определим постоянную С/ по начальным условиям. Для этого в уравнен! 5 (3) подставим значения; ^. = 0 и V-- У0 = 0:
Откуда
Для нахождения выражения скорости I/ подставим'значение С., в уравнение (Г } к выш-лниы некоторые преобразования: разделив сэременные и проинтегрировав /г получим
По начальным условиям определим Сг Для этого в уравнение (5) подсевам £ к 0 и X = «0: '
i Подставив в уравнение (5) значение Сг, получим уравнение падения зерна в конечном виде:
б)
Массивный яок спрессованного сена спускают по наклонной плоскости без начальной скорости. Определить время £ движения центра чшвстА тюка после того, как он продет путь £ «=
BHIJRIIpR
из начала отсчэта nposeoнH' од,:':/ иг- кОЙ5!#ЧШИ^:-г«1-*-..г. од-.;*•: ?.. Записать начальные уело* да; ^^^йа^й'^йедИ-. Начальные условия определим? гамъ&як® twї'ї ii «• •.«••■-уд в начальный ssoueiix движения, т.<-. вйппге-к».: при f, *0 x їX<Ў, y-..CJ0! Ц- = bfer, Ц,. l'V-v, vї.vc:< щт ■■до X, ї/, Z '•- Kуop;иг4|"ы ТО'.£и; Уд* j Vty, V2 - проекции скорс оягл, о. вообразить •дзаг&щуюсь ю-чяу в произвольном положений к указать асе действующие на то» ку силы, включая иреакции точку, находящуюся под действием силы тяжести и силы с сир •■. Яитои воздуха, поопорционаяьной первой степени скорости;; дай /? вКГпУ, где А" - постоянный коэффициент, определи заь'иН падения зерна.
Решение
Выберем начало отсчета О в начальном подожки \ Л/с, на и направим координатную ось ОХ в сторону двяжепич (Вниз). а/ альнои точки.. Для этого подсчитать Су. мы проекций сил.на координат» оси!: подставить эти су-^-ы в прг ныв час т.!.ди^..ренциалькы; уравнений движения точки: т-^А... 5-аг.? *
з$ю-
При в тем шдо обязателыз все переменные -'силы выразить через те- величины (£., x, У),"от которые они '.зависят. Проинтегрировать дифферэицнельнне уравнгтия..:;: 6. Используя начальные условия, определить постоянны!-: ?. Найти искомые в зедача-'валич.-:ны.
задача,»: <;
При сортировке гороха аеруь падают на 'решете по •-.ерти.ч-акн. "•'"■.в начальной скорости. Принимая;саа.дое зорко.ае Muн •••нальну» •..
Рис I« Запишем начальные условия движения материальной точки (зерна). При Т •§ б ха - 0, т.к. начадьнса положение точк-' //0 совпадает с'*аачалом координат. Ус -0, т.к. движение зерна начинается без начальной скорости. • йеобраз-им зерно в произвольном положения М (рис.- I) и нанесем векторы сил,,действующих на него: силу тяжегтя Р направим вняв; силу.сопротивления % неправим вверх (против движсьиг',. Подсчитаем сумму проб^цнй сил на ось X: ■ •, ■ ' ^гнх - ^ п > а 'затем, подс'авиз в правую «тасть уравнения 11 ш% -• < п*х, •получим дифференц;«8льоо& уравнение движения то?чк:
Пренде тзи решить урвш:н©ни'в (1)'.,. подстав к;-- в него R * ит У.
|



 реакцию связи N - пөрпөңшъ /лярн» к жадобу. Равлоким Силу А на две составляющих»«и'ор» /| и подсчитаем
реакцию связи N - пөрпөңшъ /лярн» к жадобу. Равлоким Силу А на две составляющих»«и'ор» /| и подсчитаем вует сила сопротивление среды Я, зависящая от скорости V бряк'-зта. Трение на этом участке пренебрежимо мало. В точке В брикет, не изменяя величины своей скорости, переходят на учес-ток ВС, где на него кромэ силы тяжести действует сила трения (коэффициент трэния / = 0,4) и переменная сила Г, проекция которой £ задана. Считая брикет мат-риаяьной точкой и знак вреш ^удлшекия брикета от точки А, до дачки В, найти закон движения брикета на участке ВС, т.е. х = /(1), где X - ВС,
вует сила сопротивление среды Я, зависящая от скорости V бряк'-зта. Трение на этом участке пренебрежимо мало. В точке В брикет, не изменяя величины своей скорости, переходят на учес-ток ВС, где на него кромэ силы тяжести действует сила трения (коэффициент трэния / = 0,4) и переменная сила Г, проекция которой £ задана. Считая брикет мат-риаяьной точкой и знак вреш ^удлшекия брикета от точки А, до дачки В, найти закон движения брикета на участке ВС, т.е. х = /(1), где X - ВС,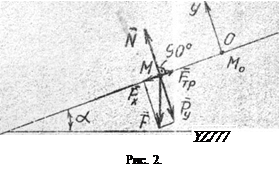 X
X




