Способы задания движения точки
Движение точки может быть задано одним из трех способов. 1. Векторный способ. Пусть точка М движется по отношению к некоторой системе отсчета Oxyz. Положение точки в любой момент времени можно определить, задав ее радиус-вектор
  . (3.2.1) . (3.2.1)
Это и есть закон движения точки в векторной форме. 2. Координатный способ. Положение точки можно непосредственно определять ее координатами, изменяющимися при движении с течением времени
 Это - закон движения точки в прямоугольных декартовых координатах. Это - закон движения точки в прямоугольных декартовых координатах.
3. Естественный способ. Задать движение точки естественным способом – это задать (рисунок 3.2) ее траекторию, начало отсчета на траектории с указанием направлений отсчета и закон движения в виде
Скоростью точки в данный момент времени t называется величина
Ускорением точки в данный момент времени t называют векторную величину, к которой стремится
т.е., вектор ускорения точки в данный момент времени равен первой производной от вектора скорости или второй производной от радиуса-вектора точки по времени
Билет8. Определение скорости и ускорения точки при координатном способе задания движения. Используем следующую теорему: проекция производной от вектора на ось, неподвижную в данной СО, равна производной от проекции дифференцируемого вектора на ту же ось. Тогда для проекций скорости имеем
или т.е., проекции скорости точки на координатные оси равны первым производным от проекций соответствующих координат точки по времени. Для проекций ускорения имеем
или
Билет9. Оси естественного трехгранника. Числовое значение скорости. Касательное и нормальное ускорения точки.
|

 (рисунок 3.1) как функцию от времени t
(рисунок 3.1) как функцию от времени t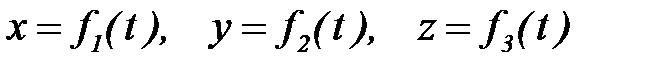 . (3.2.2)
. (3.2.2) .
. , так что скорость есть первая производная от вектора
, так что скорость есть первая производная от вектора  .
. при стремлении промежутка времени Dt к нулю
при стремлении промежутка времени Dt к нулю .
.
 .
. ,
,  ,
, 
 , т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от координат точки по времени.
, т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от координат точки по времени.


