Дифференциальные уравнения движения материальной точки
Рассмотрим движение МТ под действием сил { Проецируя уравнение
проецируя на декартовы оси, получаем ДУД точки в декартовых координатах
ДУД применяются к решению двух основных задач динамики МТ: 1-я основная задача: по движению точки найти приложенную к ней силу. Здесь нужно продифференцировать уравнения движения МТ и результаты подставить в (4.1.4) или (4.1.5), откуда определяется приложенная к точке сила; 2-я основная задача: по силам, приложенным к точке, найти ее движение. Решая эту задачу, нужно в общем случае найти вторые интегралы дифференциальных уравнений (4.1.4) или (4.1.5). В частных случаях возможно интегрирование ДУД точки, применяя метод разделения переменных.
Билет16. Количество движения точки. Импульс силы. Теорема об изменении количества движения точки. Законы динамики справедливы только в инерциальной СО. Рассмотрим движение МТ относительно СО, которая движется произвольно относительно инерциальной СО. Рассмотрим движение точки P под действием сил {
Подставим (4.3.1) в равенство (4.1.5) и преобразуем его
Примем обозначения
и Векторы Равенство (6.6) можно записать в виде
Уравнение (4.3.4) называют основным уравнением динамики относительного движения МТ. Уравнения относительного движения МТ составляются также, как в случае абсолютного движения, если к числу действующих сил добавить переносную и кориолисову силы инерции. Наблюдатель, который находится в движущейся неинерциальной системе отсчета, воспринимает переносную и кориолисову силы инерции, как реально существующие силы. Но это неверно, так как в неинерциальной СО законы механики Ньютона не действуют, и рассматривать явления с точки зрения предыдущих аксиом нельзя. Частные случаи основного уравнения относительного движения МТ: а) при поступательном переносном движении
б) при прямолинейном и равномерном переносном движении
Уравнения (4.3.6) и (4.1.2) совпадают, так как в) в относительном состоянии покоя
Это уравнение относительного равновесия МТ.
|

 } относительно инерциальной СО Оxyz, считая, что среди сил имеются реакции связей.
} относительно инерциальной СО Оxyz, считая, что среди сил имеются реакции связей.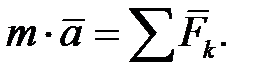 на естественные оси, получаем естественные дифференциальные уравнения движения (ДУД)
на естественные оси, получаем естественные дифференциальные уравнения движения (ДУД) ; (4.1.4)
; (4.1.4) (4.1.5)
(4.1.5)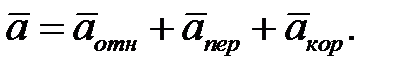 (4.3.1)
(4.3.1) (4.3.2)
(4.3.2)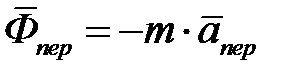 (4.3.3)
(4.3.3)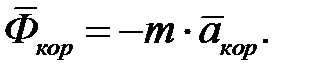 (4.3.4)
(4.3.4)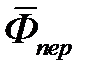 и
и  называют соответственно переносной и кориолисовой силами инерции.
называют соответственно переносной и кориолисовой силами инерции. (4.3.4)
(4.3.4) (4.3.5)
(4.3.5)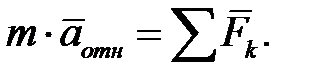 (4.3.6)
(4.3.6) . Следовательно, данная система отсчета инерциальная. Механическими опытами невозможно установить, неподвижна ли система отсчета, или она движется поступательно, равномерно и прямолинейно (принцип относительности Галилея);
. Следовательно, данная система отсчета инерциальная. Механическими опытами невозможно установить, неподвижна ли система отсчета, или она движется поступательно, равномерно и прямолинейно (принцип относительности Галилея); (4.3.7)
(4.3.7)


