Теорема об изменении кинетического момента
При движении механической системы ее кинетический момент Ко изменяется с течением времени. Чтобы установить закон изменения кинетического момента, продифференцируем по времени обе части выражения
определяющего кинетический момент:
Билет18. Работа силы. Мощность. Теорема об изменении кинетической энергии точки. Элементарной работой силы dW = Ft ∙ds, где Ft — проекция силы ds — модуль элементарного перемещения точки М. Т.к. ds = |d
 . .
т.е., элементарная работа силы равна скалярному произведению силы на вектор элементарного перемещения точки ее приложения. Работа силы на конечном перемещении M0M1 (рисунок 4.1) определяется как
Мощностью называют величину, равную работе, совершаемой силой в единицу времени. Если работа совершается равномерно, то мощность P = W/t1 (здесь t1 - время, течение которого произведена работа W). В общем случае
т.е., мощность равна произведению касательной составляющей силы на скорость. Кинетической энергией (КЭ) точки называют скалярную величину
Билет19. Механическая система. Силы внешние и внутренние. Масса системы. Центр масс. Дифференциальные уравнения движения системы.
|


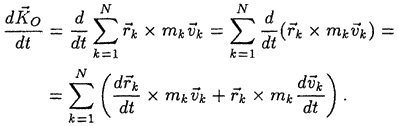
 , приложенной в точке М (рисунок 4.1), называют скалярную величину
, приложенной в точке М (рисунок 4.1), называют скалярную величину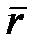 | (здесь d
| (здесь d 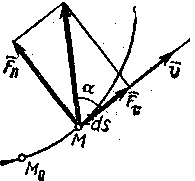
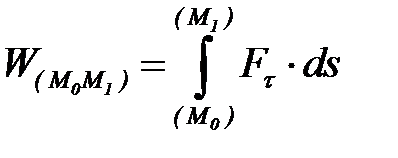 ,
, .
.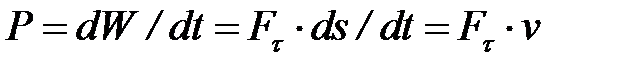 ,
, . Теорема: изменение КЭ точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.
. Теорема: изменение КЭ точки при некотором ее перемещении равно алгебраической сумме работ всех действующих на точку сил на том же перемещении.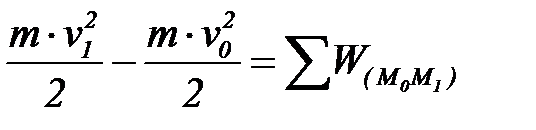 .
.


