Механическая система. Масса, центр масс и моменты инерцииМеханической системой (МС) называют совокупность взаимодействующих МТ или тел. Материальное тело является МС составляющих его частиц. МС, движение точек которой не ограничено связями, называется системой свободных материальных точек. Внешними силами Массой системы называют сумму масс частиц системы M=Σmk. Положение центра масс системы (т. С) определяется по формулам
Для тела имеем
В однородном поле силы тяжести центры масс и тяжести совпадают. Моментами инерции МС относительно оси и точки называют величины Jl=Σmk∙hk2. JO=Σmk∙rk2 где hk и rk – расстояние точки тела с массой mk от оси l иточки O. Для твердого тела момент инерции относительно оси и точки
Моменты инерции относительно декартовых осей и начала координат Jx=Σmk∙(yk2+zk2), Jy=Σmk∙(xk2+zk2), Jz=Σmk∙(xk2+yk2), JO=Σmk∙rk2= Σmk∙∙(xk2+yk2+zk2), Моменты инерции относительно координатных плоскостей равны Jxy=Σmk∙ zk2, Jyz=Σmk∙xk2, Jxz=Σmk∙yk2. Имеются зависимости 2JO= Jx+ Jy+ Jz, JO= Jxy+ Jyz+ Jxz. Для тела моменты инерции определяются интегралами по массе
Теорема Гюйгенса-Штейнера: момент инерции системы Jz относительно какой-либо оси z равен сумме момента инерции системы JzC относительно параллельной ей оси zC, проходящей через центр масс, и произведения массы системы M на квадрат расстояния между осями d
Среди семейства параллельных осей момент инерции относительно оси, проходящей через центр масс - наименьший.
|
, k= 1,2 …,n называют силы, c которыми на точки системы действуют тела, не принадлежащие к этой системе. Внутренними силами называют силы 
, k= 1,2 …,m, c которыми взаимодействуют точки системы. Можно показать, главный вектор и главный момент системы системы внутренних сил равны нулю. Отсюда не вытекает, что внутренние силы уравновешиваются в общем случае, т.к. они могут вызывать перемещения точек системы (уравновешиваются в АТТ).
,
.
,
.
,
.
, 
, 
.
.
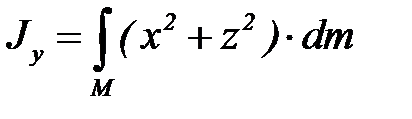