Тема: Великие математики.

уголовно-исполнительного права,

Доцент А.Г Блинов

Пояснительная записка

 

Методическое пособие по предмету математика разработана согласно: «Рекомендации по реализации образовательной программы среднего (полного) общего образования (приказ МО РФ от 30.06.99 № 56) в образовательных учреждениях НПО, в соответствии с федеральным стандартом, базисным учебным планом (МО РФ от 17.03.05 №АФ 59/03) и примерными учебными планами для образовательных учреждений Российской Федерации, реализующих программы общего образования» (МО России от 29.05.07 № 03-1180) математика в учреждениях НПО изучается с учетом профиля получаемого профессионального образования.

Программа предназначена для реализации государственных требований к самостоятельной работе студентов по ФГОС по профессии «Автомеханик», «Сварщик» и «Мастер по обработке цифровой информации» (технический профиль), «Повар, кондитер» (естественнонаучный профиль).

Назначение предмета «математика» заключается в формировании математического мышления, логики и осознания важности теоретических знаний по предмету в профессиональной деятельности.

В результате выполнения самостоятельных (внеаудиторных) работ студент должен:

Знать:

понятие функции; понятие стереометрии; понятие корпя n-й степени; понятие параллельных плоскостей; вид показательной функции; понятие логарифма числа; вид графиков основных элементарных функций; вид графика логарифмической и тригонометрической функций;

Уметь:

- оформлять реферат;

- правильно составлять опорный конспект;

- готовить логически построенное сообщение по названной теме;

- решать задачи;

- строить график функции;

- работать с интернетом по поиску информации;

- создавать и защищать презентацию.

 

Содержание:

Темы

Стр.

№1 Тема:Великие математики. (6 час.) №2 Тема: Уравнения 1 и 2 степени (2 час.) №3 Тема: Уравнения, решаемые разложением на множители (2 час.) №4 Тема: Метод интервалов решения неравенств (2 час.) №5 Тема: Уравнения и неравенства с переменной под знаком модуля (2 час.) №6 Тема: Аксиомы стереометрии (1 час.) №7 Тема: Взаимное расположение прямых в пространстве (3 час.) №8 Тема: Нахождение области определения функции по формуле (3 час.) №9 Тема: Исследование линейной функции (2 час.) №10 Тема: Исследование квадратичной функции (2 час.) №11 Тема: Стереометрия в жизни.(5час) №12 Тема: Двучленные уравнения (3час) №13 Тема: Иррациональные уравнения с переменной под знаком модуля (3час) №14 Тема: Двугранный угол (1час) №15 Тема: Показательные уравнения и неравенства (2час) №16 Тема: Показательные неравенства (2час) №17 Тема: Показательная функция (3час) №18 Тема: Логарифмические формулы (2час) №19 Тема: Решение логарифмических уравнений и неравенств (3час) №20 Тема: Логарифмическая функция (3час) №21 Тема: Математический кроссворд (3 час.) №22 Тема: Основы теории вероятности (5 час.) №23 Тема: Решение комбинаторных задач (5 час.) №24 Тема: Многогранники (1 час.) №25 Тема: Виды многогранников (4 час.) №26 Тема: Площадь боковой и полной поверхностей многогранников (4 час.) №27 Тема: Градусное и радианное измерение углов (4 час.) №28 Тема: Определения тригонометрических функций (1 час.) №29 Тема: Преобразование тригонометрических выражений (1 час.) №30 Тема: Периодичность, четность тригонометрических функций (2 час.) №31 Тема: Вычисление значений тригонометрических функций (2 час.) №32 Тема: Графики тригонометрических функций (2 час.) №33 Тема: Простейшие тригонометрические уравнения (3 час.) №34 Тема: Функция синус, косинус и их свойства (3 час.) №35 Тема: Тригонометрические функции в жизни (6 час.) №36 Тема: Тела вращения (6 час.) №37 Тема: Цилиндр (3 час.) №38 Тема: Конус (3 час.) №39 Тема: Шар (3 час.) №40 Тема: Объемы тел вращения (3 час.) №41 Тема: Моделирование (3 час.) №42 Тема: Математический кроссворд (4 час.)     ........................................................................................................................... №43 Тема: Сложение и умножение вектора на число (2 час.) №44 Тема: Формула расстояния между двумя точками (2 час.) №45 Тема: Производные элементарных функций (3 час.) №46 Тема: Экстремумы функций (5 час.) №47 Тема: Решение задач на нахождение экстремумов (3 час.) №48 Тема: Первообразная. Интеграл (4 час.) №49 Тема: Площадь криволинейной трапеции (4 час.) №50 Тема: Решение задач по профилю специальности (6 час.)

 

Тема: Великие математики.

Цель работы: Сформировать навык поиска, анализа, систематизации материала по теме, а также овладеть умением последовательно, логично и аргументировано излагать в письменном виде полученные знания, выражать собственную позицию и подтверждать её доказательствами и рассуждениями научно характера.

Задание Написать реферат на тему: «Ученые, внесшие свой вклад в становление математики» по выбору:

1. Архимед

2. Карл Фридрих Гаусс

3. Рене Декарт

4. Мстислав Всеволодович Келдыш

5. Софья Васильевна Ковалевская

6. Андрей Николаевич Колмогоров

7. Николай Иванович Лобачевский

8. Джон фон Нейман

9. Исаак Ньютон

10. Пифагор

11. Лев Семенович Понтрягин

12. Леонард Эйлер

13. Башмаков, Марк Иванович

14. Анри Пуанкаре

15. Егоров, Дмитрий Фёдорович

16. Жегалкин, Иван Иванович

17. Колмогоров, Андрей Николаевич

18. Лобачевский, Николай Иванович

19. Ушаков, Владимир Николаевич

20. Чебышев, Пафнутий Львович

 

Реферат должен содержать титульный лист представленный в приложении 1, фотографию ученого, краткие биографические сведения, заслуги его как математика. В конце представленного материала должен быть указан источник информации, где были взяты сведения. Например Интернет ресурс:

http://ru.wikipedia.org/wiki/Ньютон,-Исаак.

№2 Тема: Уравнения 1 и 2 степени.

Цель: Продолжить формирования навыка решения уравнений 1 и 2 степени.

Задание 2. Решить уравнения:

a)

b)

c)

d)

e)

 

 

№3 Тема: Уравнения, решаемые разложением на множители.

Цель: Продолжить формирования навыка решения уравнений.

Задание 2. Решить уравнения:

a)

b)

 

 

№4 Тема: Метод интервалов решения неравенств.

Цель: Продолжить формирования навыка решения уравнений.

Задание 2. Решить уравнения:

a)

b)

 

 

№5 Тема: Уравнения и неравенства с переменной под знаком модуля (2 час)

Цель: Продолжить формирования навыка решения уравнений.

Задание 2. Решить уравнения:

 

a)

b) |x-1|=2

c) |x+2|=4

d) |x-1|=|x-2|

 

 

 

№6 Тема: Аксиомы стереометрии.

Цель: Продолжить формирования навыка запоминания текста.

Задание 1. Вставьте пропущенные слова.

 

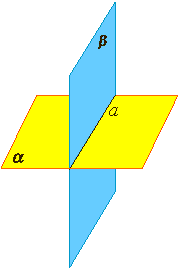
Стереометрия — это раздел ______________, в котором изучаются свойства фигур в пространстве.

Аксиомы стереометрии и их следствия

Аксиома 1.

Через любые _____ точки, не лежащие на одной прямой, проходит ________, и притом только одна.

Аксиома 2.

Если ____ точки прямой лежат в плоскости, то все точки ______ лежат в этой плоскости. (Прямая лежит на ______ или плоскость проходит через прямую).

Аксиома 3.

Если две различные плоскости имеют общую _______, то они имеют общую _________, на которой лежат все общие точки этих плоскостей. В таком случае говорят, плоскости пересекаются по ________.

Теорема 1.

Через прямую a и не лежащую на ней точку А проходит ___________, и притом только одна.

Теорема 2.

Через две _____________ прямые a и b проходит _________, и при том только одна.

 

Задание 2. Поставьте в соответствие аксиомы и рисунки к ним.

№7 Тема: Взаимное расположение прямых в пространстве».

Цель: Решение задач по теме: «Взаимное расположение прямых в пространстве»

Задание. Решить задачу № 121 (учебник Геометрия 10-11, Л. С. Атанасян).

 

 

№8 Тема: Нахождение области определения функции по формуле.

Цель: Продолжить формирования навыка анализа.

Задание. Найти область определения функции по формуле:

a)

b)

 

c)

d)

 

№9 Тема: Исследование линейной функции

Цель:

• Обобщить и систематизировать знания обучающихся о свойствах функции: область определения и область значений функции, нули, наибольшее и наименьшее значение функции, возрастание и убывание.
• Закрепить умение учащихся по формуле функции находить её область определения.
• Закрепить умение по графику читать основные свойства функции.
• Закрепить умение выполнять построение графика и исследовать функцию.

Задание. Исследовать график функции y(x) по схеме, указанной в ПРИЛОЖЕНИИ 2.

Варианты:

a)

b)

№10 Тема: Исследование квадратичной функции.

Цель:

• Обобщить и систематизировать знания обучающихся о свойствах функции: область определения и область значений функции, нули, наибольшее и наименьшее значение функции, возрастание и убывание.
• Закрепить умение учащихся по формуле функции находить её область определения.
• Закрепить умение по графику читать основные свойства функции.
• Закрепить умение выполнять построение графика и исследовать функцию.

Задание. Исследовать график функции y(x) по схеме, указанной в ПРИЛОЖЕНИИ 2..

Варианты: ; .

 

 

№11 Тема: Стереометрия в жизни.

Цель:

• Обобщить и систематизировать знания обучающихся о свойствах геометрических фигур в пространстве.
• Сформировать навык поиска, анализа, систематизации материала в глобальной сети Интернет по теме.
• Овладеть умением последовательно, логично и красочно представлять материал в виде презентации.

 

Задание 3. Создать презентацию средствами программы MS PowerPoint или Open Office Impress, на тему: «Стереометрия в природе и архитектуре».

Презентация в первом слайде должна содержать информацию о теме, группе и фамилии обучающегося, а также информацию об источнике (см рисунок).

Рис. 1 Титульный слайд презентации.

 

Количество слайдов - от 5 до 10. Иллюстрации приветствуются. Оценивается соответствие темы доклада и дизайн программного продукта.

Критерий оценивания:

Оценка «3» – выполнено 5 слайдов без фотографий (или не соответствующих теме) и ошибки в оформлении презентации;

Оценка «4» - выполнено от 5 до 10 слайдов, с небольшими ошибками в оформлении и фотографиями;

Оценка «5» - выполнено 10 и более слайдов, без ошибок в оформлении и с фотографиями по теме презентации.

 

 

№ 12, 13 Тема: Решение иррациональных уравнений и неравенств.

Цель:

• Продолжить формирование умений решения иррациональных уравнений и неравенств.

 

Задание Решить уравнения и неравенства.

вариант	задание	вариант	задание
	;		;
	;		;
	;		;
	;		;
	;		;

 

Пример 1. Решить уравнение

Решение.

Возведем обе части уравнения в квадрат. x² - 3 = 1;
Перенесем -3 из левой части уравнения в правую и выполним приведение подобных слагаемых. x² = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.

Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение.
Проверка.
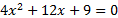
При x₁ = -2 - истинно:
При x₂ = -2 - истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.