Рассмотрим тонкий изолированный стержень, лежащий на отрезке  оси
оси  . Предположим, что его физические свойства в точках любого сечения одинаковы. Тогда температура тела есть функция от абсциссы
. Предположим, что его физические свойства в точках любого сечения одинаковы. Тогда температура тела есть функция от абсциссы 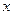 сечения и времени
сечения и времени  :
:
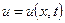 ,
, 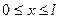 ,
, 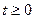
Можно показать, что функция 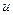 удовлетворяет дифференциальному уравнению в частных производных
удовлетворяет дифференциальному уравнению в частных производных
 , где
, где 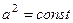 (1)
(1)
Найдем решение уравнения (1), удовлетворяющее
а) начальному условию
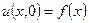 , (2)
, (2)
где 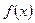 – заданная на отрезке
– заданная на отрезке  непрерывная функция,
непрерывная функция,
б) граничным условиям
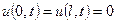 (3)
(3)
То есть предполагается, что в начальный момент времени температура в стержне выражается функцией 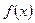 , а на протяжении всего времени опыта на концах искусственно поддерживается нулевая температура.
, а на протяжении всего времени опыта на концах искусственно поддерживается нулевая температура.
Будем решать задачу (1)-(3) методом Фурье, т.е. найдем нетривиальные решения в виде
 (4)
(4)
Подставляя функцию (4) в уравнение (1), получим
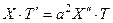
или
 .
.
Левая часть этого равенства зависит только от 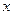 , правая – только от
, правая – только от  , поэтому
, поэтому
 , где
, где 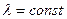 .
.
Таким образом, функции 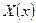 и
и  удовлетворяют обыкновенным дифференциальным уравнениям
удовлетворяют обыкновенным дифференциальным уравнениям
 (5)
(5)
 (6)
(6)
Вследствие граничных условий (3) получим
 ,
,
 .
.
Отсюда
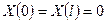 (7)
(7)
Мы пришли к задаче: найти такие числа  , для которых дифференциальное уравнение (5) имеет нетривиальное решение на отрезке
, для которых дифференциальное уравнение (5) имеет нетривиальное решение на отрезке  , удовлетворяющее граничным условиям (7).
, удовлетворяющее граничным условиям (7).
Эта задача называется проблемой Штурма–Лиувилля.
Числа  называются собственными значениями задачи, а соответствующие нетривиальные функции, удовлетворяющие условиям (7) – собственными функциями, удовлетворяющими этим условиям.
называются собственными значениями задачи, а соответствующие нетривиальные функции, удовлетворяющие условиям (7) – собственными функциями, удовлетворяющими этим условиям.
Пусть  , тогда общее решение уравнения (5) запишется так:
, тогда общее решение уравнения (5) запишется так:
 .
.
Используя условие (7), найдем коэффициенты  и
и  ,:
,:
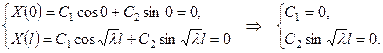
Так как  , то
, то


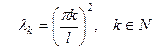 .
.
Каждому собственному значению 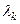 соответствуют собственные функции задачи Штурма–Лиувилля:
соответствуют собственные функции задачи Штурма–Лиувилля:
 .
.
Решим уравнение (6) при найденных 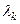
 ,
,
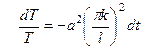 ,
,
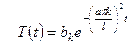 ,
,
где 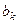 – произвольная постоянная.
– произвольная постоянная.
Итак,  – частные решения уравнения (1), удовлетворяющие условию (3).
– частные решения уравнения (1), удовлетворяющие условию (3).
Тогда и сумма ряда
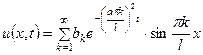
при достаточно малых 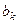 будет удовлетворять уравнению (1) и граничным условиям (3).
будет удовлетворять уравнению (1) и граничным условиям (3).
Найдем коэффициенты 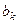 , пользуясь начальным условием:
, пользуясь начальным условием:

 (8)
(8)
Формула (8) представляет собой разложение в ряд Фурье функции 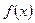 , поэтому коэффициенты
, поэтому коэффициенты 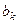 вычисляются по формуле
вычисляются по формуле
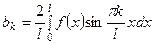 .
.
Таким образом, решение задачи (1)–(3) имеет вид:
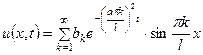 , где
, где 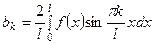

 оси
оси  . Предположим, что его физические свойства в точках любого сечения одинаковы. Тогда температура тела есть функция от абсциссы
. Предположим, что его физические свойства в точках любого сечения одинаковы. Тогда температура тела есть функция от абсциссы 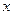 сечения и времени
сечения и времени  :
: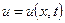 ,
, 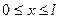 ,
, 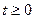
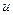 удовлетворяет дифференциальному уравнению в частных производных
удовлетворяет дифференциальному уравнению в частных производных , где
, где 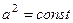 (1)
(1)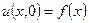 , (2)
, (2)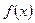 – заданная на отрезке
– заданная на отрезке 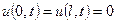 (3)
(3) (4)
(4)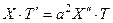
 .
. , где
, где 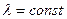 .
.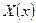 и
и  удовлетворяют обыкновенным дифференциальным уравнениям
удовлетворяют обыкновенным дифференциальным уравнениям (5)
(5) (6)
(6) ,
, .
.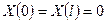 (7)
(7) , для которых дифференциальное уравнение (5) имеет нетривиальное решение на отрезке
, для которых дифференциальное уравнение (5) имеет нетривиальное решение на отрезке  , тогда общее решение уравнения (5) запишется так:
, тогда общее решение уравнения (5) запишется так: .
. и
и  ,:
,: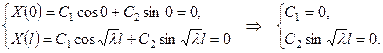
 , то
, то

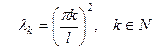 .
.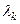 соответствуют собственные функции задачи Штурма–Лиувилля:
соответствуют собственные функции задачи Штурма–Лиувилля: .
. ,
,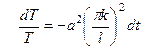 ,
,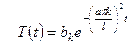 ,
,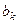 – произвольная постоянная.
– произвольная постоянная. – частные решения уравнения (1), удовлетворяющие условию (3).
– частные решения уравнения (1), удовлетворяющие условию (3).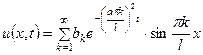

 (8)
(8)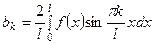 .
.


