Решение уравнения колебаний струны методом Фурье
Найдем решение уравнения
в области
Суть метода Фурье или метода разделения переменных заключается в отыскании решения задачи (1)-(3) в виде
Будем искать нетривиальные решения, т.е.
Отсюда
Подставляя функцию (4) в уравнение (1), получим
или
Функция от
Получим два обыкновенных дифференциальных уравнения
Найдем значения Составим характеристическое уравнение для уравнения (6):
Если Пусть
Найдем
Пусть
Отсюда
Общее решение уравнения (7) при найденных
Тогда решение уравнения (1) имеет вид
Тогда и любые суммы Если ряд
Определим коэффициенты
Формулы (9) и (10) представляют собой разложения функций Коэффициенты разложения определяются по формулам
Итак, решение задачи (1)-(3) определяется рядом (8), коэффициенты которого определяются по формулам (11). Пример. Решить уравнение колебания струны методом Фурье.
Решение. Находим
Интеграл
Тогда
В результате получим
Окончательно получим Таким образом, искомая функция имеет вид
|

 , (1)
, (1)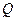 , удовлетворяющее следующим условиям
, удовлетворяющее следующим условиям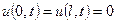 (2)
(2) (3)
(3) (4)
(4)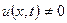 , удовлетворяющие граничным условиям
, удовлетворяющие граничным условиям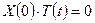 ,
,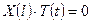 для всех
для всех  .
.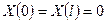 (5)
(5)
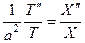 .
.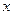 равна функции от
равна функции от  , только если обе они равны постоянному числу. Обозначим его через
, только если обе они равны постоянному числу. Обозначим его через 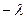 , т.е.
, т.е.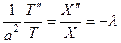 .
. (6)
(6)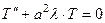 (7)
(7) , при которых задача имеет нетривиальное решение. Если такие решения существуют, то
, при которых задача имеет нетривиальное решение. Если такие решения существуют, то 
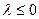 , то
, то 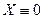 .
. , тогда общее решение уравнения (6) имеет вид
, тогда общее решение уравнения (6) имеет вид .
. и
и  , используя условие (5):
, используя условие (5):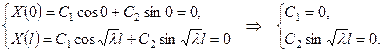
 , тогда
, тогда
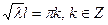 .
.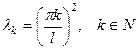 .
.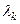 – собственные значения,
– собственные значения,  – собственные функции – решения уравнения (6).
– собственные функции – решения уравнения (6).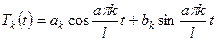 .
.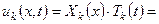
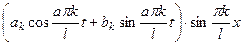 .
.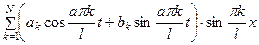 есть решение уравнения (1), удовлетворяющие граничным условиям (5)
есть решение уравнения (1), удовлетворяющие граничным условиям (5)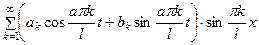 равномерно сходится в области
равномерно сходится в области 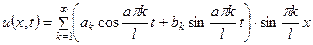 (8)
(8)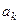 и
и 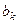 , используя начальные условия (3):
, используя начальные условия (3):
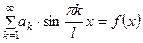 (9)
(9)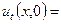
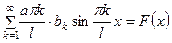 (10)
(10)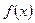 и
и 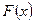 по синусам на отрезке
по синусам на отрезке  .
.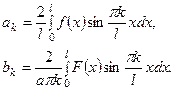 (11)
(11)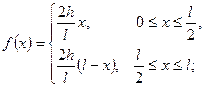
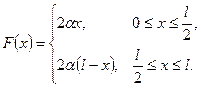
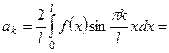

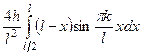 .
. берем по частям;
берем по частям;  ,
, 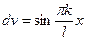 ,
, 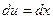 ,
, 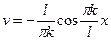 ; следовательно
; следовательно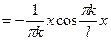
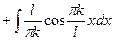
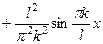 .
.
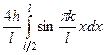
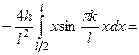

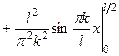




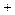
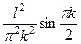
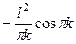
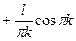
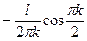

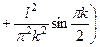 .
.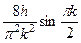 . Находим
. Находим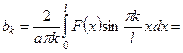
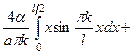


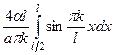
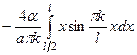 .
.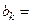
 .
.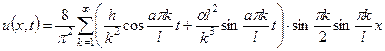 .●
.●


