Вывод уравнения колебаний струны
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Струной называется тонкая нить, работающая на растяжение, но не на изгиб. Это значит, если мысленно разрезать струну в точке Пусть концы натянутой струны закреплены в точках В момент времени Будем рассматривать малые, плоские, поперечные колебания струны около положения равновесия, совпадающего с осью
Выделим отрезок
Пусть
Так как колебания малые, то
Проекция силы
Сумма этих проекций на ось
По теореме Лагранжа (о конечном приращении) получим
С другой стороны, по закону Ньютона, сила, действующая на рассматриваемый элемент струны, равна
отсюда
Тогда
Сокращая на
или
Уравнение (1) называется уравнением свободных колебаний однородной струны. Это уравнений имеет бесконечное множество решений, поэтому только одного уравнения (1) недостаточно для полного описания движения струны. Нужны дополнительные условия, вытекающие из физического смысла задачи. Из физики известно, что для определения движения необходимо знать начальное положение и начальную скорость:
Условия (2) – начальные условия или условия Коши. Кроме того, нужно указать, что происходит на концах струны. Для закрепленной струны имеем граничные или краевые условия:
Итак, физическая задача об определении движения струны, закрепленной на концах, свелась к математической задаче: Найти такое решение уравнения (1), которое удовлетворяет начальным условиям (2) и граничным условиям (3). Эта задача называется смешанной или начальной краевой задачей для гиперболических уравнений.
|

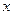 , то действие одного участка струны на другой (сила
, то действие одного участка струны на другой (сила  ) будет направлена по касательной к струне в точке
) будет направлена по касательной к струне в точке  и
и  . Плотность струны будем считать равной
. Плотность струны будем считать равной  на всем ее протяжении.
на всем ее протяжении. выведем струну из положения равновесия. Струна начнет совершать колебания. Через время
выведем струну из положения равновесия. Струна начнет совершать колебания. Через время  точка
точка 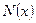 займет положение
займет положение 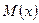 .
. величину отклонения струны от положения равновесия в точке
величину отклонения струны от положения равновесия в точке 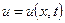 есть уравнение струны в момент времени
есть уравнение струны в момент времени 
 и рассмотрим участок струны, соответствующий этому отрезку. На концах этого участка
и рассмотрим участок струны, соответствующий этому отрезку. На концах этого участка  и
и  действуют силы натяжения
действуют силы натяжения  и
и  , направленные по касательной к кривой в соответствующих точках и равные по абсолютной величине:
, направленные по касательной к кривой в соответствующих точках и равные по абсолютной величине:
 .
. – угол между касательной к струне и положительным направлением оси
– угол между касательной к струне и положительным направлением оси  в точке
в точке  .
. , тогда проекция силы
, тогда проекция силы  равна
равна .
. .
.
 , где
, где  .
.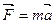 , где
, где  ,
, 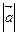
 ,
,  .
.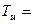

 .
. .
. и устремив
и устремив  , т.е.
, т.е. 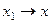 и
и  , получим
, получим
 , где
, где 
 , (1)
, (1) (2)
(2)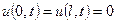 (3)
(3)


