Теоретические сведения
1) Создать следующую структуру данных, содержащую анкетную информацию о студентах своей группы:
2) В соответствии с выданным вариантом выполнить сортировку полученных данных по следующим характеристикам и направлениям:
3) Проиллюстрировать промежуточные и конечные результаты с помощью 3-4 графиков. 4) Оформить отчёт. 5) Подготовить ответы на контрольные вопросы. Закрепить материал.
Контрольные вопросы 1. Что такое структура и для чего она служат? 2. Перечислите как минимум два способа заполнения многоуровневой структуры. 3. Можно ли добавлять в структуры новые поля? 4. С помощью какой функции можно вывести имена всех полей структуры? 5. Можно ли создать пустой массив ячеек? Пустой массив структур? 6. Какую величину возвращает функция datenum? Простейшие алгоритмы шифрования
Цель: изучить основы шифрования данных, а также примеры их использования в информационных технологиях. Задачи: 1) выбрать из структуры данных соответствующую информацию; 2) произвести над полученными данными предварительную обработку; 3) произвести шифрование данных с помощью одного из указанных методов. Теоретические сведения Шифрование − способ преобразования открытой информации в закрытую и обратно. Криптография − область знаний, изучающая тайнопись (криптография) и методы ее раскрытия (криптоанализ). Цель криптографической системы заключается в том, чтобы зашифровать осмысленный исходный текст (также называемый открытым текстом, получив в результате совершенно бессмысленный на взгляд шифрованный текст, или, коротко, шифртекст (называемый также криптограммой). Получатель, которому он предназначен, должен быть способен расшифровать (говорят также "дешифровать") этот шифртекст, восстановив, таким образом, соответствующий ему открытый текст. При этом противник (называемый также криптоаналитиком) должен быть неспособен раскрыть исходный текст. Существует важное отличие между расшифрованием (дешифрованием) и раскрытием шифртекста. Раскрытием криптосистемы называется результат работы криптоаналитика, приводящий к возможности эффективного раскрытия любого, зашифрованногос помощью данной криптосистемы, открытого текста. Степень неспособности криптосистемы к раскрытию называется ее стойкостью. Существуют несколько способов, в соответствии с которыми могут классифицироваться криптографические системы. В качестве основной принимается следующая классификация криптосистем: 1. ограниченного использования; 2. общего использования; 3. с секретным ключом; 4. с открытым ключом. Считается, что криптографическая система является криптосистемой ограниченного использования, если ее стойкость основывается на сохранении в секрете самого характера алгоритмов шифрования и дешифрования. Простейшим историческим примером такой системы можно считать так называемый шифр Цезаря, который представляет из себя простую замену каждого символа открытого текста третьим следующим за ним символом алфавита. Например, слово "cleartext" превращается в "fohduwhaw". Однако, в общем случае шифр Цезаря реализуется заменой каждой буквы в сообщении другой буквой этого же алфавита, отстоящей от нее в алфавите на фиксированное число букв. В своих шифровках Цезарь заменял букву исходного открытого текста буквой, отстоящей от исходной буквы впереди на три позиции. Одним из очевидных требований обеспечения стойкости общей криптографической системы является огромное количество возможных ключей, не позволяющее провести исчепывающий поиск (в котором осуществляется попытка систематического дешифровывания заданного шифртекста, используя при этом каждый из возможных ключей до тех пор, пока не получится некий осмысленный открытый текст). Например, при наивном подходе шифр Цезаря можно рассматривать как пример общей криптосистемы (с ключом k =3), шифрование в которой заключается в замене каждого очередного символа открытого текста k -ым после него символом соответствующего алфавита, где k −; некий секретный ключ. Но такое обобщение является бесполезным, потому что оно предоставляет возможность использования лишь 25 нетривиальных ключей, и тем самым обеспечивает простоту полного перебора для любого, кто предположительно знает метод шифрования (по крайней мере, если шифрованное сообщение имеет достаточную избыточность, чтобы у него была единственная осмысленная расшифровка). Однако, для автоматической дешифрации закодированного текста методом Цезаря применяется тот факт, что вероятностное распределение определённых букв в алфавите практически всегда остаётся неизменным. Поэтому, при подсчёте частоты встречаемости всех знаков в тексте, зашифрованном методом Цезаря, каждый из них можно соотнести с соответствующим символом в конкретном алфавите. Например, в таблице №1 представлены распределения частот встречи букв в тексте для русского языка (в порядке убывания). Причём частоты следующие буквы E c Ё, Ь с Ъ отождествлены, а также имеется знак пробела (-) между словами. Таблица №1
Криптографическую систему называют криптосистемой общего использования, если ее стойкость основывается не на секретности алгоритмов шифрования и дешифрования, а на секретности некоторого сравнительно короткого значения, которое называется ее ключом. Такой ключ должен легко вырабатываться конкретными пользователями при помощи их собственных ключей таким образом, чтобы даже разработчик криптосистемы не мог раскрыть ее, не имея доступа к тому ключу, который в ней в действительности использовался. Для некоторых применений (главным образом в военных, дипломатических и разведывательных ведомствах) для разработчика общей криптосистемы нет никаких причин для того, чтобы открытым образом описывать характер ее алгоритмов. Сохраняя эту информацию в тайне, можно обеспечить даже некоторую дополнительную безопасность. Однако, решающим обстоятельством, позволяющим полагаться на такую секретность, это не является, поскольку ничего нельзя сказать о том, когда она может быть скомпрометирована. По этой причине, исследования надежности таких систем всегда должны проводиться в предположении, что потенциальному противнику о криптосистеме известно все, за исключением реально используемого секретного ключа. А если на самом деле противник такими знаниями не обладает, то это даже лучше. Для других типов применений, подобных, например, большим финансовым комплексам, в действительности лучше раскрывать, как работают их криптосистемы. В противном случае пользователи всегда будут предполагать возможность существования некоего секретного метода раскрытия такой криптосистемы. В качестве ключа в шифрующих таблицах используются: − размер таблицы; − слово или фраза, задающие перестановку; − особенности структуры таблицы. Одним из самых примитивных табличных шифров перестановки является простаяперестановка, для которой ключом служит размер таблицы. Этот метод шифрования сходен с шифром скитала. Например, сообщение ТЕРМИНАТОР ПРИБЫВАЕТ СЕДЬМОГО В ПОЛНОЧЬ записывается в таблицу поочередно по столбцам. Результат заполнения таблицы из 5 строк и 7 столбцов показан на рис. 1. После заполнения таблицы текстом сообщения по столбцам для формирования шифртекста считывают содержимое таблицы по строкам.
Если шифр записывать группами по пять букв, получается такое шифрованное сообщение: ТНПВЕ ГЛЕАР АДОНР ТИЕЬВ ОМОБТ МПЧИР ЫСООЬ Естественно, отправитель и получатель сообщения должны заранее условиться об общем ключе в виде размера таблицы. Следует заметить, что объединение букв шифртекста в 5-буквенные группы не входит в ключ шифра и осуществляется для удобства записи несмыслового текста. При расшифровании действия выполняют в обратном порядке. Несколько большей стойкостью к раскрытию обладает метод шифрования, называемый одиночной перестановкой по ключу. Этот метод отличается от предыдущего тем, что столбцы таблицы переставляются по ключевому слову, фразе или набору чисел длиной в строку таблицы. Применим в качестве ключа, например, слово Пеликан а текст сообщения возьмем из предыдущего примера. На рис.2 а и б показаны две таблицы, заполненные текстом сообщения и ключевым словом, при этом левая таблица соответствует заполнению до перестановки, а правая таблица - заполнению после перестановки.
В верхней строке левой таблицы записан ключ, а номера под буквами ключа определены в соответствии с естественным порядком соответствующих букв ключа в алфавите. Если бы в ключе встретились одинаковые буквы, они бы были пронумерованы слева направо. В правой таблице столбцы переставлены в соответствии с упорядоченными номерами букв ключа. При считывании содержимого правой таблицы по строкам и записи шифртекста группами по пять букв получим шифрованное сообщение: ГНВЕП ЛТООА ДРНЕВ ТЕЬИО РПОТМ БЧМОР СОЫЬИ Для обеспечения дополнительной скрытности можно повторно зашифровать сообщение, которое уже прошло шифрование. Такой метод шифрования называется двойной перестановкой. В случае двойной перестановки столбцов и строк таблицы перестановки определяются отдельно для столбцов и отдельно для строк. Сначала в таблицу записывается текст сообщения, а потом поочередно переставляются столбцы, а затем строки. При расшифровании порядок перестановок должен быть обратным. Пример выполнения шифрования методом двойной перестановки показан на рис. 3. Если считывать шифртекст из правой таблицы построчно блоками по четыре буквы, то получится следующее: ТЮАЕ ООГМ РЛИП ОЬСВ Ключом к шифру двойной перестановки служит последовательность номеров столбцов и номеров строк исходной таблицы (в нашем примере последовательности 4132 и 3142 соответственно).
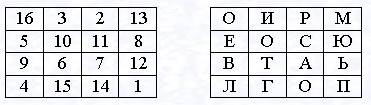
Число вариантов двойной перестановки быстро возрастает при увеличении размера таблицы: − для таблицы 3х3 36 вариантов; − для таблицы 4х4 576 вариантов; − для таблицы 5х5 14400 вариантов. Однако двойная перестановка не отличается высокой стойкостью и сравнительно просто "взламывается" при любом размере таблицы шифрования. Примером использования в шифровании особенностей структуры таблиц является применениемагических квадратов. В средние века для шифрования перестановкой применялись и магические квадраты. Магическими квадратами называют квадратные таблицы с вписанными в их клетки последовательными натуральными числами, начиная от 1, которые дают в сумме по каждому столбцу, каждой строке и каждой диагонали одно и то же число. Шифруемый текст вписывали в магические квадраты в соответствии с нумерацией их клеток. Если затем выписать содержимое такой таблицы по строкам, то получится шифртекст, сформированный благодаря перестановке букв исходного сообщения. В те времена считалось, что созданные с помощью магических квадратов шифртексты охраняет не только ключ, но и магическая сила. Пример магического квадрата и его заполнения сообщением ПРИЛЕТАЮ ВОСЬМОГО показан на рис. 4.
ПРИЛЕТАЮ ВОСЬМОГО Шифртекст, получаемый при считывании содержимого правой таблицы по строкам, имеет вполне загадочный вид: ОИРМ ЕОСЮ ВТАЬ ЛГОП Число магических квадратов быстро возрастает с увеличением размера квадрата. Существует только один магический квадрат размером 3х3 (если не учитывать его повороты). Количество магических квадратов 4х4 составляет уже 880, а количество магических квадратов 5х5 - около 250000. В системах шифрования с открытым ключом каждый пользователь выбирает свой собственный секретный ключ, на основании которого получает пару алгоритмов. Затем он делает один из них доступным каждому из возможных респондентов, объявляя этот алгоритм своим открытым алгоритмом шифрования, в то время как другой, соответствующий первому и являющийся его личным алгоритмом дешифрования, хранит в строгом секрете. Это позволяет даже совершенно незнакомому, например, с абонентом сети по имени Алиса пользователю применять ее общедоступный алгоритм шифрования, чтобы зашифровать предназначенное для нее сообщение; однако, лишь сама Алиса сможет расшифровать его после получения с помощью своего секретного алгоритма дешифрования.
|