Краткие сведения из теории

Практическая работа №1

 

Тема: Булева алгебра. Логические операции. Формулы и их преобразование.

 

Цель работы: Практическое изучение логических операций, формул и их преобразований.

 

Краткие сведения из теории

Алгебра логики - это раздел математики, изучающий высказывания, рассматриваемые со стороны их логических значений (истинности или ложности) и логических операций над ними.

Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: "1" и "0".

Основоположником математической логики является английский математик Джордж Буль (1815 – 1864). Он впервые высказал идеи логического истолкования теории множеств.

Рассмотрим 2^х элементное множество B, элементы которого 0 и 1. Однако они не являются числами в обычном смысле. Наиболее распространенная интерпретация двоичных переменных – это логические: “ДА – НЕТ” или “ИСТИННО – ЛОЖНО”. Например: в языках программирования вводится специальный тип переменной – логическая переменная, значения которой обозначаются TRUE и FALSE.

Таким образом, элементы множества B={0,1} будем рассматривать как формальные символы, а не числа.

Алгебра, образованная множеством B вместе со всеми возможными операциями на нем, называется алгеброй логики или Булевой алгеброй.

Булевой функцией f(x₁, x₂, …, x_n) называется функция, которая принимает два значения 0 или 1 в зависимости от переменных х_i, каждая из которых может также принимать только два значения 0 или 1.

В таблице наборы переменных расположены в определенном порядке, который совпадает с порядком возрастания наборов, рассматриваемых как двоичные числа. Этим упорядочиванием будем пользоваться и дальше.

Рассмотрим основные функции алгебры логики.

1. Логическое отрицание (инверсия) обозначается чертой над аргументом. Это функция одной переменной:

 

f(x) = x; 0 =1; 1=0.

 

Схема, реализующая логическое отрицание, называется логическим элементом НЕ.

Графическое обозначение элемента:

1 x

x

 

 

2. Логическое сложение (дизъюнкция). Это функция нескольких переменных. Функция обозначается следующим образом:

 

f(x₁,x₂) = x₁ V x₂ V x₃…

 

Для двух переменных таблица истинности имеет вид:

x₁ x₂ f(x₁,x₂)

0 0 0

0 1 1

1 0 1

1 1 1

Условное графическое обозначение схемы ИЛИ

x₁

1 x₁ V x₂

x₂

 

 

3. Логическое умножение (конъюнкция). Это функция нескольких переменных. Функция обозначается следующим образом:

f(x₁x₂) = x₁ /\ x₂ /\ х₃ …

 

Функция определяется следующей таблицей истинности для двух переменных.

x₁ x₂ f(x₁x₂)

0 0 0

0 1 0

1 0 0

1 1 1

Условное графическое обозначение схемы И

 

x₁ &

x₁ * x₂

x₂

 

4. Функция Шеффера – реализует умножение с отрицанием. Определяется для двух переменных следующей таблицей истинности. Это функция нескольких переменных:

 

x₁ x₂ f(x₁x₂)

0 0 1

0 1 1

1 0 1

1 1 0

 

Функция имеет вид:

f(x₁x₂) = x₁½x₂ = x₁ /\ x₂

 

Условное графическое обозначение схемы И-НЕ

x₁

& x₁ * x₂

x₂

 

 

5. Функция Пирса реализует логическое сложение с отрицанием. Определяется следующей таблицей истинности для двух переменных

 

x₁ x₂ f(x₁x₂)

0 0 1

0 1 0

1 0 0

1 1 0

 

Функция имеет вид:

f(x₁x₂) = x₁ ¯ x₂ = x₁ Ú x₂

 

Условное графическое обозначение схемы ИЛИ-НЕ

 

X1

1 x₁ Ú x₂

X2

 

 

Функции дизъюнкции и конъюнкции могут быть не только функциями двух переменных. В общем случае произвольного числа аргументов.

 

6. Сложение по mod 2. Выполняет логическую операцию XOR. Это функция нескольких переменных и определяется следующей таблицей истинности для двух переменных:

 

x1	x2	Y

 

Функция имеет вид Y =x₁ Å x₂

Условное графическое обозначение элемента исключающее ИЛИ.

x₁

=1

Y = x₁ Å x₂

x₂

 

Всякая логическая функция “n” переменных может быть задана таблицей, в левой части которой перечислены все 2ⁿ наборов значений переменных, а в правой части – значения функции на этих наборах. Например, для 3-х переменных имеем:

x1	x2	x3	Y

 

Наборы (строки) х на которых функция Y=1 называют единичным набором. Наборы х на которых Y=0, называют нулевым набором Y.

Составим логическую функцию из таблицы значений. Для этого возьмем конъюнкции аргументов в той строке, где функция равна единице. Причем, если аргумент равен нулю – он берется с инверсией. Если аргумент равен единице – он берется с без инверсии. Полученные конъюнкции соединяем дизъюнкцией. Для нашего примера имеем три конъюнкции (три строки таблицы, где функция равна единице). Логическая функция имеет вид:

Y = (X1 /\ X2 /\ X3) \/ (X1 /\ X2 /\ X3) \/ (X1 /\ X2 /\ X3)

 

Инверсия обозначается чертой над аргументом. В первой конъюнкции аргументы Х1, Х2 взяты с инверсией, так как их значения во второй строке таблицы равны нулю. Во второй конъюнкции аргументы Х2, Х3 взяты с инверсией, так как их значения в пятой строке таблицы равны нулю. В третьей конъюнкции аргумент Х2 взят с инверсией, так как его значение в шестой строке таблицы равно нулю. Полученные конъюнкции объединены операциями дизъюнкции.

 

Основные законы алгебры логики

 

1. Переместительный закон. Коммутативность (лат. – менять, переменять).

X₁ Ú X₂ = X₂ Ú X₁ X₁ Ù X₂ = X₂ Ù X₁

 

2. Сочетательный закон. Ассоциативность (лат. – соединять).

X₁ Ú (X₂ Ú X₃) = (X₁ Ú X₂) Ú X₃

X₁ Ù (X₂ Ù X₃) = (X₁ Ù X₂) Ù X₃

 

3. Распределительный закон. Дистрибутивность.

X₁ Ù (X₂ Ú X₃) = (X₁ Ù X₂) Ú (X₁ Ù X₃)

X₁ Ú (X₂ Ù X₃) = (X₁ Ú X₃) Ù (X₁ Ú X₃)

 

4. Закон поглощения.

X₁ Ú (X₁ ÙX₂) = X₁ X₁ Ù(X₁ Ú X₂) = X₁

 

5. Закон склеивания.

X₁X₂ Ú X₁X₂ = X₁ (X₁ Ú X₂)(X₁ Ú X₂) = X₁

 

6. Правило де Моргана.

X₁ Ú X₂ Ú X₃ = X₁ X₂ X₃; X₁X₂X₃ = X₁ Ú X₂ Ú X₃

 

Выполнение логических операций производится в соответствии с приоритетами. В таблице представлены приоритеты выполнения логических операций.

приоритет	операция
	инверсия конъюнкция дизъюнкция сложение по mod 2

 

Операции одного приоритета выполняются слева направо. Для изменения порядка выполнения операций могут использоваться скобки.

Содержание работы

 

1. Выбрать вариант в задании 1 из таблицы 1 и составить логическую функцию. Для первого варианта берутся значения Y1, для второго варианта берутся значения Y2 и т.д.

2. Преобразовать логическую функцию к более простому виду.

3. Проверить полученную логическую функцию подстановкой нулей и единиц для аргументов Х1, Х2, Х3.

4. Выбрать вариант в задании 2 и найти значение логического выражения.

5. Выбрать вариант в задании 3 и по заданной принципиальной схеме составить логическое выражение и заполнить для него таблицу истинности.

6. Отчет о проделанной работе выполнить в документе Microsoft Word под титульным листом (Приложение1).

 

Задание 1

 

Таблица 1. Варианты заданий

 

X1

X2

X3

Y1

Y2

Y3

Y4

Y5

Y6

Y7

Y8

Y9

Y10

 

Продолжение таблицы 1

 

Y11	Y12	Y13	Y14	Y15	Y16	Y17	Y18	Y19	Y20

Задание 2. Найти значение приведённых ниже логических выражений:

 

1) A AND B OR NOT C при A = False, B = True, C = False;

 

2) (x < y) AND (x = z) при a) x = 0, y = 0, z = 0;

б) x = 0, y = -8, z = 0.

3) (a £ z) OR (z>2) OR (a ≠ 5) при a) a = 5, z = -4;

б) a = -5,z = 0.

4) (x ≠ y) OR (z < 4) при a) x = 5, y = 7, z = 0;

б) x = 5, y = -7, z = 10.

5) (x ≠ y) AND (z < 4) при a) x = 5, y = 7, z = 0;

б) x = 5, y = -7, z = 10;

6) NOT (x > z) при a) x = 5, z = -2;

б) x = -5, z = 2;

7) NOT A OR B при A = True, B = False;

 

8) (A OR B) AND C при A = True, B = False, C = True;

 

9) (x ≥ y) OR (z > -4) при a) x = 5, y = 7, z = 0;

б) x = 5, y = -7, z = 10;

10) (x ≥ y) OR (z ≤ 4) при a) x = 5, y = 7, z = 0;

б) x = 5, y = -7, z = 10;

б) x = 2, z = 2;

11) A OR NOT B при A = False, B = False;

 

12) A OR B AND C при A = True, B = False, C = True;

 

13) (x ≥ y) OR (z > -4) при a) x = 5, y = 7, z = 0;

б) x = 5, y = -7, z = 10;

14) (x ≤ y) AND (z ≤ 4) при a) x = -5, y = -7, z = 0;

б) x = 5, y = -7, z = 10;

б) x = 2, z = 2;

15) A AND NOT B при A = True, B = False;

 

16) NOT (A OR B) AND C при A = True, B = False, C = True.

 

17) A OR B AND NOT C при A = False, B = True, C = False;

 

18) (x < y) OR (x = z) при a) x = 0, y = 0, z = 0;

б) x = 0, y = -8, z = 0;

 

19) (a £ z) AND (z>2) AND (a ≠ 5) при a) a = 2, z = 4;

б) a = -5,z = 0;

 

20) A £ B при a) A = 2, B = 2;

при б) A = 2, B = 2;

 

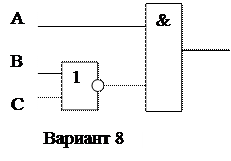
Задание 3

 

По заданной принципиальной схеме составить логическое выражение и заполнить для него таблицу истинности.

 

Вариант 1 Вариант 2

Вариант 9

Вариант 10

 

Содержание отчета

1. Постановка задачи.

2. Краткие сведения из теории.

3. Результаты выполненных заданий.

4. Ответы на контрольные вопросы.

Контрольные вопросы

 

1. Дайте определение Булевой функции.

2. Назовите основные функции алгебры логики.

3. Составить таблицу истинности для функции Пирса.

4. Какие значения может принимать Булева функция?

5. Составить таблицу истинности для функции Шеффера.

6. Какой вид имеет функция Пирса?

7. Составьте таблицу истинности для логической операции XOR.

8. Найти значение функции Y=x1×x2Úx1×x2 при х1=0,х2=1.

9. Перечислите основные законы алгебры логики.

10. Какая логическая операция имеет высший приоритет?

11. Напишите переместительный закон для двух аргументов.

12. Найти значение функции Y=x1×x2Úx1×x2 при х1=1,х2=1.

13. Найти значение функции Y=x1×x2Úx1×x2 при х1=1,х2=1.

14. Напишите сочетательный закон для двух аргументов.

Приложение 1: