Булева алгебра и логические схемы компьютера. Логические машины.
Булева алгебра, созданная в середине 18 века Дж. Булем, оперирует с логическими переменными. Основополагающим законом булевой алгебры является закон исключения третьего, согласно которому логические переменные, в отличие от переменных обычной алгебры, могут принимать только два значения {«да», «нет»}, {«истинно», «ложно»} и т.д. Переменные обычно обозначаются, как и двоичные цифры, символами 0 и 1. Булева алгебра – алгебра, образованная множеством В={0, 1} вместе со всеми возможными логическими операциями на нём. Булева (логическая) функция – это функция, принимающая значения 0 или 1 в результате логических операций над логическими переменными. Операции над переменными записываются с помощью символов: &, ∨, –, ⊕, → и т.д. Булева функция может быть задана: 1) словесным описанием (назначением, определением), 2) таблицей истинности, 3)формулой, состоящей из букв, знаков логических операций и скобок, 4)комбинационной схемой, составленной из логических элементов, 5)координатным способом (картой Карно), 6)переключательной схемой, 7)диаграммой Венна, 8) геометрическим способом (гиперкубами), 9)диаграммой двоичного решения и т.д. 5 9)Основы логики: логика высказываний, логические языки, таблица истинности 10)Графы и деревья 11)Обзор и история архитектуры компьютеров 9) Основы логики: логика высказываний, логические языки, таблица истинности Логика высказываний (или пропозициональная логика от англ. propositional logic, или исчисление высказываний [1]) — это формальная теория, основным объектом которой служит понятие логического высказывания. С точки зрения выразительности, её можно охарактеризовать как классическую логику нулевого порядка. Несмотря на свою важность и широкую сферу применения, логика высказываний является простейшей логикой и имеет очень ограниченные средства для исследования суждений[ Логический язык программирования — Логическое программирование парадигма программирования, основанная на автоматическом доказательстве теорем, а также раздел дискретной математики, изучающий принципы логического вывода информации на основе заданных фактов и правил вывода. Под «логической функцией» в данном случае понимается функция, у которой значения переменных (параметров функции) и значение самой функции выражают логическую истинность. Например, в двузначной логике они могут принимать значения «истина» либо «ложь» ( Табличное задание функций встречается не только в логике, но для логических функций таблицы оказались особенно удобными, и с начала XX века за ними закрепилось это специальное название. Особенно часто таблицы истинности применяются в булевой алгебре и в аналогичных системах многозначной логики.
|

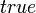 либо
либо 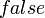 ,
, 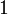 либо
либо 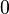 ).
).


