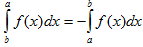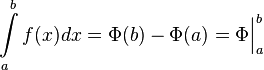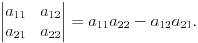Вопрос 6. Свойства неопределенного интеграла
Свойства неопределенного интеграла В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f и a, k, C − постоянные величины.
Вопрос 7
Вопорос 8 Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка Геометрический смысл определенного интеграла- это площади криволинейной трапеции,ограниченной графиком.
Вопрос 9 I. Величина определенного интеграла не зависит от обозначения переменной интегрирования, т.е. II. Определенный интеграл с одинаковыми пределами интегрирования равен нулю.
III. При перестановке пределов интегрирования определенный интеграл меняет свой знак на обратный.
IV. Если промежуток интегрирования [a,b] разбит на конечное число частичных промежутков, то определенный интеграл, взятый по промежутке [a,b], равен сумме определенных интегралов, взятых по всем его частичным промежуткам.
V. Постоянный множитель можно выносить за знак определенного интеграла.
VI. Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций.
Формула Ньютона-Лейбница:
Вопрос 10 1. Площадь плоской фигуры. Площадь фигуры, ограниченной графиком непрерывной функции y = f (x)(f (x)≥0), двумя прямыми x = a и x = b и осью Ox, или площадь криволинейной трапеции, ограниченной дугой графика функции y = f (x), a ≤ x ≤ b (рис. 1) вычисляется по формуле S =∫ abf (x) dx. Площадь фигуры, ограниченной графиками непрерывных функций y = f 1(x) и y = f 2(x), f 1(x)≤ f 2(x) и двумя прямыми x = a, x = b (рис. 2) определяется по формуле S =∫ ab (f 2(x)− f 1(x)) dx.
Если фигура ограничена кривой, имеющей параметрические уравнения x = x (t), y = y (t), прямыми x = a, x = b и осью Ox, то площадь ее вычисляется по формуле S =∫ t 1 t 2 y (t) x ′(t) dt =∫ t 1 t 2 y (t) dx (t),(1) где пределы интегрирования находятся из уравнений a = x (t 1), b = x (t 2)(y (t)≥0 на отрезке [ t 1, t 2]). Формула (1) применима также для вычисления площади фигуры, ограниченной замкнутой кривой (изменение параметра t от t 1 до t 2 должно соответствовать обходу контура по часовой стрелке). Площадь фигуры, ограниченной графиком непрерывной функции r = r (φ;) и двумя лучами φ;= α;, φ;= β;, где φ; и r − полярные координаты, или площадь криволинейного сектора, ограниченного дугой графика функции, r = r (φ;), α;≤ φ;≤ β;, вычисляется по формуле S =12∫ αβr 2 dφ;. Вопрос 11 Определителем второго порядка называется число равное разности произведений элементов главной и второй диагонали: Примеры определителей второго порядка: Определителем третьего порядка называется следующее выражение: Определитель третьего порядка вычислить легко, если учесть следующее правило: со знаком плюс идут произведения троек чисел, расположенных на главной диагонали матрицы, и в вершинах треугольников с основанием параллельным этой диагонали и вершиной в противоположного угла матрицы. Со знаком минус идут тройки из второй диагонали и из треугольников, построенных относительно этой диагонали. Следующая схема демонстрирует это правило, называемое правилом треугольников. В схеме синим (слева) отмечены элементы, чьи произведения идут со знаком плюс, а зеленым (справа) - со знаком минус. Примеры определителей третьего порядка: Вопрос 12
|





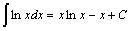











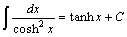
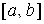 на частичные отрезки, ни от выбора точек
на частичные отрезки, ни от выбора точек  в них, то этот предел называется определенным интегралом от функции
в них, то этот предел называется определенным интегралом от функции  на отрезке
на отрезке 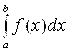
 , где х, t – любые буквы.
, где х, t – любые буквы.