Упражнения. Установите, какие из указанных функций являются ДНФ, КНФ, СДНФ и СКНФ:
- Установите, какие из указанных функций являются ДНФ, КНФ, СДНФ и СКНФ:
а.  ; ;
б.  ; ;
в.  ; ;
г.  ; ;
д.  ; ;
е.  ; ;
ж.  . .
- Постройте ДНФ для следующих с помощью равносильных преобразований:
а. 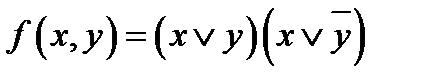 ; ;
б. 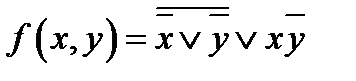 . .
- Постройте КНФ с помощью равносильных преобразований:
а. 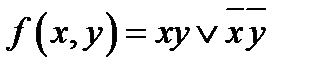 ; ;
б.  . .
- Постройте для функции
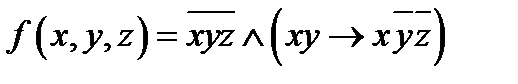 СДНФ и СКНФ с помощью равносильных преобразований. СДНФ и СКНФ с помощью равносильных преобразований. - Постройте СДНФ и СКНФ для функции
 с помощью таблицы истинности. с помощью таблицы истинности. - Постройте канонический многочлен Жегалкина для функции
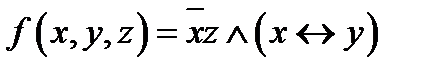 методом элементарных преобразований. методом элементарных преобразований. - Постройте канонический многочлен Жегалкина для функции
 методом неопределенных коэффициентов. методом неопределенных коэффициентов. - Используя равносильные преобразования, построить ДНФ, КНФ, СДНФ и СКНФ для следующих функций:
а.  ; ;
б. 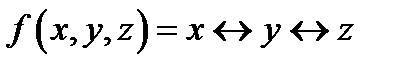 ; ;
в. 
- Используя формулы разложения Шеннона, постройте СДНФ и СКНФ для следующих функций:
а. 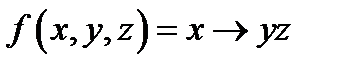 ; ;
б.  ; ;
в. 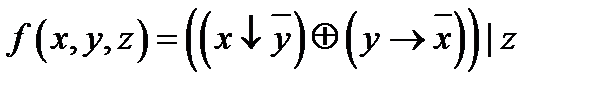
- Построить ДНФ и КНФ для функции
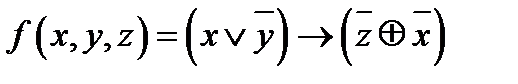 . . - Используя равносильные преобразования, построить СДНФ для функции

- Постройте СКНФ для заданной функции, используя двойственное предельное разложение Шеннона:
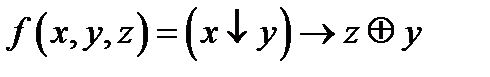 . .
- Методом равносильных преобразований найти канонический многочлен Жегалкина для функции

- Найти канонический многочлен Жегалкина методом неопределенных коэффициентов для функции
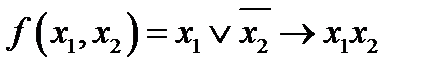 . .
- Используя равносильные преобразования, построить ДНФ, КНФ, СДНФ и СКНФ для следующих функций:
а.  ; ;
б. 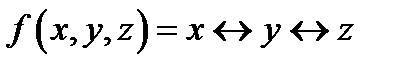 ; ;
в. 
- Используя формулы разложения Шеннона, постройте СДНФ и СКНФ для следующих функций:
а. 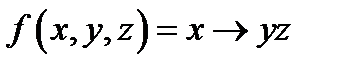 ; ;
б.  ; ;
в. 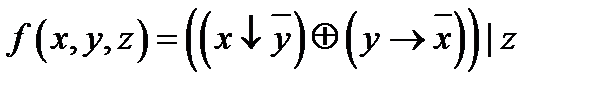
- С помощью эквивалентных преобразований постройте для функции
 ДНФ, КНФ, СДНФ, СКНФ. ДНФ, КНФ, СДНФ, СКНФ. - Методом равносильных преобразований найти канонический многочлен Жегалкина:
а.  ; ;
б.  ; ;
в.  . .
- Найти канонический многочлен Жегалкина для следующих функций, используя метод неопределенных коэффициентов:
а.  ; ;
б.  ; ;
в. 

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|

Кардиналистский и ординалистский подходы Кардиналистский (количественный подход) к анализу полезности основан на представлении о возможности измерения различных благ в условных единицах полезности...
|

Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит. Multisim оперирует с двумя категориями...
|

Композиция из абстрактных геометрических фигур Данная композиция состоит из линий, штриховки, абстрактных геометрических форм...
|
Уравнение волны. Уравнение плоской гармонической волны. Волновое уравнение. Уравнение сферической волны Уравнением упругой волны называют функцию , которая определяет смещение любой частицы среды с координатами относительно своего положения равновесия в произвольный момент времени t...
Медицинская документация родильного дома Учетные формы родильного дома № 111/у Индивидуальная карта беременной и родильницы
№ 113/у Обменная карта родильного дома...
Основные разделы работы участкового врача-педиатра Ведущей фигурой в организации внебольничной помощи детям является участковый врач-педиатр детской городской поликлиники...
|
Эндоскопическая диагностика язвенной болезни желудка, гастрита, опухоли Хронический гастрит - понятие клинико-анатомическое, характеризующееся определенными патоморфологическими изменениями слизистой оболочки желудка - неспецифическим воспалительным процессом...
Признаки классификации безопасности Можно выделить следующие признаки классификации безопасности.
1. По признаку масштабности принято различать следующие относительно самостоятельные геополитические уровни и виды безопасности.
1.1. Международная безопасность (глобальная и...
Прием и регистрация больных Пути госпитализации больных в стационар могут быть различны. В центральное приемное отделение больные могут быть доставлены:
1) машиной скорой медицинской помощи в случае возникновения острого или обострения хронического заболевания...
|
|