Матрица, размерность матрицы, единичная матрица. Нехай дана система лінійних однорідних рівнянь
Нехай дана система лінійних однорідних рівнянь
Очевидно, що однорідна система завжди сумісна ( При яких умовах однорідна система має і ненульові розв'язки?
Теорема.1.4.4. Для того, щоб система однорідних рівнянь мала ненульові розв'язки, необхідно і достатньо, щоб ранг її основної матриці був меншим числа
□ Необхідність Оскільки не може перевищувати розмір матриці, то, очевидно,
Достатність. Нехай Нехай дана однорідна система з
Теорема.1.4.5 Для того, щоб однорідна система □ Якщо система має ненульові розв'язки, то
Приклад 1.4.6. Розв’язати систему:
○
Поклавши
Матрица, размерность матрицы, единичная матрица. Матрицей называется прямоугольная таблица чисел, состоящая из m одинаковой длины строк или n одинаковой длины столбцов. Количество строк и столбцов матрицы задают размер матрицы Единичная матрица - это диагональная матрица, у которой каждый элемент на главной диагонали равен единице.
|


 ), вона має нульовий (тривіальний) розв'язок
), вона має нульовий (тривіальний) розв'язок  .
. невідомих, тобто
невідомих, тобто 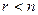 .
. . Нехай
. Нехай  , тоді один з мінорів розміру
, тоді один з мінорів розміру  відмінний від нуля. Тому відповідна система лінійних рівнянь має єдиний розв'язок:
відмінний від нуля. Тому відповідна система лінійних рівнянь має єдиний розв'язок:  . Тобто, інших, крім тривіальних, розв’язків немає. Отож, якщо є нетривіальні розв'язки, то
. Тобто, інших, крім тривіальних, розв’язків немає. Отож, якщо є нетривіальні розв'язки, то  невідомими:
невідомими: ■
■ дорівнював нулю:
дорівнював нулю:  .
. система має тільки єдиний, ненульовий розв'язок. Якщо ж
система має тільки єдиний, ненульовий розв'язок. Якщо ж  основної матриці системи менше числа невідомих, тобто
основної матриці системи менше числа невідомих, тобто 


 ,
,  . Оскільки
. Оскільки 
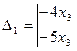

 Тобто,
Тобто,  - загальний розв'язок.
- загальний розв'язок.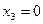 , отримаємо один частинний розв'язок
, отримаємо один частинний розв'язок  . Поклавши
. Поклавши  , отримаємо другий частинний розв'язок
, отримаємо другий частинний розв'язок  і т.д. ●
і т.д. ●


