Асимптоты
Асимптота – прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность
1) Вертикальная асимптота Вертикальная асимптота – прямая вида х=а при условии существования предела
При определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон.
2) Горизонтальная асимптота Горизонтальная асимптота – прямая вида у=а при условии существ. предела Горизонтальная асимптота является частным видом наклонной при
3) Наклонная асимптота
Наклонная асимптота – прямая вида y=kx+b при условии существования пределов: 1. 2.
Прямая y=kx+b называется наклонной асимптотой графика функции y=f(x), если f(x) можно представить как kx+b+α(x), где α(x) – бесконечно малая функция при х→
Замечания: 1) Функция может иметь не более двух наклонных (горизонтальных) асимптот 2) Если хотя бы один из двух упомянутых выше пределов не существует (или равен 3) Функция имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту, или одну наклонную и одну горизонтальную, или две наклонных, или две горизонтальных, либо же вовсе не имеет асимптот
|


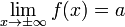
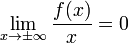 (коэфф. k)
(коэфф. k)

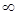
 ), то наклонной асимптоты при
), то наклонной асимптоты при  (или
(или  ) не существует
) не существует


