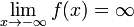I замечательный предел и его следствия
Следствия: 1) Предел x/sin(x) при х→0 = 1 2) Предел tg(x)/x при х→0 = 1 (доказательство: tg(x)/x = sin(x)/x * 1/cos(x), тогда предел [1*1]=1) 3) Предел arcsin(x)/x при х→0 = 1 (доказательство: t=arcsin(x), тогда sin(x)=t, и предел arcsin(x)/x равен пределу t/sin(t) = 1) 4) Предел arctg(x)/x x при х→0 = 1 (доказательство аналогично предыдущему) 5) Предел (1-cos(x))/x2 при х→0 = 0.5 (доказательство: (1-cos(x))/x2 = (2sin2(x/2))/x2; предел (2sin2(x/2))/x2 при х→0 = предел sin(x/2)/x * sin(x/2)/x * 2/4 = 0.5)
Следствия (википедия):
II замечательный предел и его следствия
Следствия: 1) = предел ln(1+x) 1/x = ln предела (1+x) 1/x = ln(e) = 1) 2) = предел t/ ln(t+1) = 1)
Следствия (википедия):
Бесконечно малые и бесконечно большие функции. Сравнение бесконечно малых
1) Функция называется бесконечно малой при х→х0 если предел f(x) при х→х0 = 0 2) Функция называется бесконечно большой при х→х0 если предел f(x) при х→х0 =
Предел ех при х→ - Предел ех при х→ +
Бесконечно малая величина Функция называется БМ, если Функция называется БМ в окрестности точки x0, если Функция называется БМ на бесконечности, если Бесконечно большая величина Функция называется ББ, если Функция называется ББ в окрестности точки x 0, если Функция называется ББ на бесконечности, если
|

 (неопределенность [0/0])
(неопределенность [0/0])

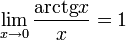

 (неопределенность 1
(неопределенность 1 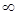 ) (е=2,7 приближенно)
) (е=2,7 приближенно)
 ([0/0] доказательство: предел ln(1+x)/x = предел 1/x* ln(1+x) =
([0/0] доказательство: предел ln(1+x)/x = предел 1/x* ln(1+x) = (доказательство: предел (ex-1)/x = [t = ex-1; ex = t+1; x=ln(t+1)] =
(доказательство: предел (ex-1)/x = [t = ex-1; ex = t+1; x=ln(t+1)] =

 для
для  ,
, 




 либо
либо 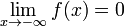


 либо
либо