СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ
Векторные поля - отображения одного векторного пространства в другое. Скалярные поля - функции на векторном пространстве.
Диссипативная функция (функция рассеяния) — функция, вводимая для учёта перехода энергии упорядоченного движения в энергию неупорядоченного движения, в конечном счёте — в тепловую (такой переход, например, имеет место при воздействии на механическую систему сил вязкого трения). Диссипативная функция характеризует скорость убывания (рассеяния) механической энергии системы и имеет размерность мощности. Диссипативная функция, делённая на абсолютную температуру, определяет скорость, с которой возрастает энтропия (мера неопределённости какого-либо опыта (испытания)) в системе. Уравнения Навье-Стокса - система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости, состоящая из уравнения движения (векторное уравнение, выражающее баланс импульса для сплошной среды.) и уравнения неразрывности (оно выражает собой закон сохранения массы в элементарном объёме, то есть непрерывность потока жидкости или газа). Часто уравнениями Навье-Стокса называют только одно векторное уравнение движения. В векторном виде для несжимаемой жидкости они записываются следующим образом:
где
Оператор набла Для трёхмерного евклидова пространства в прямоугольной декартовой системе координат оператор набла определяется следующим образом:
где Если вектор
который представляет собой градиент функции Если вектор
то есть дивергенция вектора Если вектор
Векторный оператор Лапласа Векторный оператор Лапласа действует на векторное поле и имеет векторное значение, тогда как скалярный лапласиан действует на скалярное поле и имеет скалярное значение. При вычислении в декартовых координатах, получаемое векторное поле эквивалентно векторному полю скалярного Лапласиана, действующего на отдельные компоненты исходного вектора. Векторный оператор Лапласа некоторого векторного поля 1) Через оператор набла: 2) Через градиент, дивергенцию и ротор: Градиент (растущее поле) – определяет направление и скорость скорейшего возрастания скалярного поля (скаляр-вектор). Например, если взять в качестве С математической точки зрения градиент — это производная скалярной функции, определенной на векторном пространстве (рис. 3.1).
Пространство, на котором определена функция и её градиент, может быть, вообще говоря, как обычным трёхмерным пространством, так и пространством любой другой размерности любой физической природы или чисто абстрактным. Использовав единичные вектора по осям прямоугольных декартовых координат
Дивергенция (расхождение) – линейный дифференциальный оператор, характеризующий расходимость, источники и стоки векторного поля (вектор-скаляр). Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением С точки зрения физической интерпретации (и в строгом смысле, и в смысле интуитивного физического образа математической операции) дивергенция векторного поля является показателем того, в какой степени данная точка пространства (точнее достаточно малая окрестность точки) является источником или стоком этого поля (рис. 3.2):
Согласно геометрической интерпретации, если в качестве векторного поля (на двумерном пространстве) взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причём на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся). Ротор (вихрь) - векторный дифференциальный оператор, характеризует вихревую составляющую векторного поля (вектор-вектор).
Для удобства можно формально представлять ротор как векторное произведение оператора набла (слева) и векторного поля:
Лапласиан – сочетание дивергенции и градиента (скаляр-скаляр):
Ротор и дивергенция - для векторных полей. Градиент, лапласиан - для скалярных полей.
Тензор - объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Тензор обычно обозначают некоторой буквой с совокупностью верхних (контрвариантных) и нижних (ковариантных) индексов: В качестве примера тензор механического напряжения второго ранга, компоненты которого в трёхмерной декартовой системе координат образуют матрицу представлен в следующем виде:
столбцами которой являются силы, действующие на
- Тензор ранга (0,0) есть скаляр - величина, каждое значение которой может быть выражено одним числом; - Тензор ранга (1,0) есть вектор (контравариантный вектор) - это элемент пространства - Тензор ранга (0,1) есть ковектор (ковариантный вектор), то есть элемент пространства, которое изоморфно проекции (отображение точек пространства на его подпространство любой размерности)
Касательное расслоение
В линейной алгебре, ковариантный вектор на векторном пространстве - это то же самое, что и линейный функционал на этом пространстве В дифференциальной геометрии, ковариантный вектор на дифференцируемом многообразии это гладкое сечение кокасательного расслоения - Тензор ранга (0,2) есть билинейная форма, например, метрический тензор (это симметричное тензорное поле ранга (0,2) на гладком многообразии, посредством которого задаются скалярное произведение векторов в касательном пространстве, длины кривых, углы между кривыми и т. д.), например - Тензор ранга (1,1) есть линейный оператор Линейный оператор - обобщение линейной числовой функции
|

 , (3.1)
, (3.1) - оператор набла (оператор Гамильтона),
- оператор набла (оператор Гамильтона),  - векторный оператор Лапласа,
- векторный оператор Лапласа, 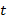 - время,
- время,  - коэффициент кинематической вязкости,
- коэффициент кинематической вязкости,  - плотность,
- плотность,  - давление,
- давление, - векторное поле скоростей,
- векторное поле скоростей,  - векторное поля массовых сил (т.е. сил, действующих на каждый элементарный объём вещества и пропорциональных массе вещества, заключённого в этом объёме - силы тяготения, силы инерции и т.д.).
- векторное поля массовых сил (т.е. сил, действующих на каждый элементарный объём вещества и пропорциональных массе вещества, заключённого в этом объёме - силы тяготения, силы инерции и т.д.). (оператор Гамильтона) - векторный дифференциальный оператор, компоненты которого являются частными производными по координатам.
(оператор Гамильтона) - векторный дифференциальный оператор, компоненты которого являются частными производными по координатам. , (3.2)
, (3.2) - единичные векторы (орты) по осям
- единичные векторы (орты) по осям  соответственно.
соответственно. , то получится вектор:
, то получится вектор: , (3.3)
, (3.3) , получится скаляр:
, получится скаляр: , (3.4)
, (3.4) .
. (3.5)
(3.5)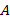 определяется следующим образом:
определяется следующим образом: ;
; .
. высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.
высоту поверхности земли над уровнем моря, то её градиент в каждой точке поверхности будет показывать «направление самого крутого подъёма», и своей величиной характеризовать крутизну склона.
 , получаем следующее
, получаем следующее . (3.6)
. (3.6)
 - точка поля является источником;
- точка поля является источником; - точка поля является стоком;
- точка поля является стоком; - стоков или источников нет либо они компенсируют друг друга.
- стоков или источников нет либо они компенсируют друг друга.
 . (3.7)
. (3.7) . (3.8)
. (3.8) . При смене базиса (системы координат) ковариантные компоненты меняются так же, как и базис (с помощью того же преобразования), а контравариантные - обратно изменению базиса (обратным преобразованием).
. При смене базиса (системы координат) ковариантные компоненты меняются так же, как и базис (с помощью того же преобразования), а контравариантные - обратно изменению базиса (обратным преобразованием).
 грани исследуемого куба.
грани исследуемого куба.
 , которое изоморфно (наличие биекции – взаимно-однозначного отображения (соответствия)) пространству
, которое изоморфно (наличие биекции – взаимно-однозначного отображения (соответствия)) пространству  ;
; ;
;
 ,
,  , и т.д.
, и т.д. или
или 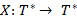 .
. .
.


