Лаг (lag) - расстояния, которые выбираются для поиска пар точек при расчете моментов второго порядка (вариограммы): .
Лаг (lag) - расстояния, которые выбираются для поиска пар точек при расчете моментов второго порядка (вариограммы):. Опорные точки, отстоящие друг от друга на расстояние, меньшее, чем радиус влияния, пространственно коррелируют, в то время как точки, отстоящие друг от друга на расстояние, большее, чем радиус влияния, - нет. Порог (sill) - параметр теоретической модели вариограммы, характеризующий значение вариограммы на большом расстоянии, в конечной точке радиуса влияния (при условии ее стационарности). Т.е. это обычно величина дисперсии значений. Когда вариограмма достигает порога, она часто выполаживается, т.е. больше не растет. Радиус корреляции, ранг (range) - параметр теоретической модели вариограммы, характеризующий расстояние, на котором достигается постоянное значение (порог) вариограммы. Эффект "самородка" (nugget effect) - остаточный, пространственно не коррелированный шум (вариации ошибок измерения в совокупности с пространственными вариациями для расстояний, значительно меньших шага Поведение вначале (эффект самородка и наклон) играет критическую роль в подборе модели вариограммы. Это случайная составляющая дисперсии исследуемых данных, которая измеряет насколько велико различие содержаний в очень близко расположенных значениях. Величина ЭС зависит от сети опробования исходных данных и степени их изменчивости. Наклон можно оценить по первым трем - четырем значениям вариограммы. Эффект самородка можно оценить экстраполяцией кривой в начало системы координат. Радиус влияния обычно можно оценить визуально. Порог характеризуется значением, где вариограмма стабилизируется (становится горизонтальной). Для стационарных переменных порог совпадает с общей дисперсией проб, но иногда это не верно, так как в исходных данных присутствуют тренды большой протяженности. Если присутствует более одной зоны влияния (несколько структур), то вспомогательные зоны можно различить визуально в местах, где вариограмма меняет кривизну. Существуют два типа направленных составляющих, которые должны быть устранены перед созданием модели вариограммы: глобальные тренды и анизотропия. Глобальный тренд - это доминирующий процесс, который оказывает детерминистское влияние на все измерения. Глобальный тренд может быть представлен математической формулой (например, полиномом) и вычтен из значений в опорных точках, а затем вновь добавлен после выполнения интерполяции. Этот процесс носит название «вычитание (или удаление) тренда». Анизотропия – это неоднородность свойств по разным направлениям. Различают геометрическую (аффинную) и зональную анизотропию.
Рис.2.3. Пример геометрической (аффинной) анизотропии
Вариограммы, построенные для разных направлений имеют приблизительно одинаковый уровень порога, но разные зоны влияния. Геометрическую анизотропию можно устранить путём аффинных преобразований (заданием эллипса анизотропии, короткая ось которого совпадает с направлением наибольшей изменчивости, а длинная – с направлением наименьшей).
Рис. 2.4. Пример зональной анизотропии Вариограммы, построенные для разных направлений, выходят на пороги разного уровня. Способ устранения зональной анизотропии зависит от причин её появления. Причиной зональной анизотропии может быть зональное строение толщи, использование данных, полученных по разным основаниям, эффект пропорциональности и т.д. При зональном строении толщи можно попытаться выделить отдельные зоны и анализировать их раздельно. Если анизотропия связана с эффектом пропорциональности, можно перейти к так называемым относительным вариограммам. В них, вместо полудисперсии используется своеобразный коэффициент вариации, который получается в результате деления значений каждой локальной вариограммы на квадрат локального среднего содержания и затем усреднения полученных величин в процессе подгонки вариограммной модели. Существуют статистические моменты, аналогичные вариограмме, но отличающиеся степенью, в которую возводится разница значений пар точек. 1. Мадограмма (madogram) - модуль разницы - позволяет уменьшить влияние больших разбросов значений по сравнению с вариограммой:
2. Родограмма (rodogram) - квадратный корень - еще более понижает влияние значений с большим разбросом:
3. Дрейф (drift) - очень важная функция при анализе пространственной корреляции:
В отличие от вариограммы дрейф не обладает точечной симметрией. Дрейф может служить указателем правомочности предположения о внутренней гипотезе для данных. Такой вывод можно сделать, если значение Это может, в частности, означать, что у данных имеется систематический тренд, т.е. определенная зависимость значения исследуемой функции от пространственного местоположения (координаты). Для таких данных моделирование вариограммы и использование обычных геостатистических оценивателей может привести к необоснованным результатам. И для ковариации, и для вариограммы существуют стандартизованные варианты: коррелограмма и стандартизованная вариограмма. Эти моменты второго порядка являются более робастными, т.е. более устойчивыми к зашумленным данным и присутствию выбросов (outliers). Они вычисляются по следующим формулам:
4. Коррелограмма (correlogram):
5. Стандартизованная вариограмма (standardised variogram):
где
Очень часто в реальных данных наблюдается эффект пропорциональности, при появлении зависимости между средним Этот эффект можно с помощью вычисления локальных статистических характеристик - среднего и вариации, когда последнее (вариация) демонстрирует явное детерминированное поведение:
где
Для этого используется метод движущегося окна. Статистика движущегося окна ( Метод состоит в разбиении области данных на несколько одинаковых, обычно прямоугольных окрестностей - окон. Размер окна зависит от среднего расстояния между точками. Хорошим компромиссом между большими и маленькими окнами являются перекрывающиеся окна. При этом два соседних окна имеют несколько общих точек. Это повышает количество окон при достаточно большом их размере, дающем достоверную статистику. Таким образом, мы как бы берем в руки «окно-лупу» и рассматриваем всю область, передвигая по ней окно. Статистические характеристики вычисляются для каждого поднабора данных, попавших в отдельное окно. При наличии эффекта пропорциональности предлагается использовать относительные вариограммы, которые нивелируют (устраняют особенности) эффект пропорциональности. Можно выделить два вида относительных вариограмм (
6. Общая относительная вариограмма (
когда вариограмма просто нормируется на квадрат среднего значения данных, разделенных вектором
7. Парная относительная вариограмма (pairwise relative variogram):
когда нормировка на квадрат среднего производится для каждой конкретной пары данных отдельно. Функции для моделирования вариограмм должны обладать определёнными свойствами. В перечень допустимых функций входят: Линейная, Круговая, Сферическая, Тетрасферическая, Пентасферическая, Экспоненциальная, Логарифмическая, Гауссова, Рациональная квадратическая, Модель с эффектом дыр, Базовая синусоидальная модель. 1. Линейная функция вариограммы:
2. Сферическая функция вариограммы:
3. Логарифмическая функция вариограммы:
4. Квадратичная функция вариограммы:
5. Круговая функция вариограммы:
6. Экспоненциальная функция вариограммы:
7. Гауссова функция вариограммы:
Для тех случаев, если
Здесь
Для зависимостей 1,3,6,7 порог
Выбор параметров Наличие эффекта самородка обычно хорошо определяется по графику выборочной вариограммы (при подходе к нулю функция стремится к некоторой константе, отличной от нуля). В связи с этим, часто при автоматическом выборе параметров значение фиксируют Начальное значение радиуса влияния обычно выбирают равным значению Иногда применяют и нелинейные методы оптимизации для одновременного поиска всех параметров Правильному выбору типа модельной вариограммы может помешать наличие глобального тренда в исходных данных. Выборочная вариограмма при этом обычно все время возрастает с ростом В таких случаях необходимо строить тем или иным способом (обычно методом наименьших квадратов) тренд по опорным точкам, последовательно увеличивая его степень, вычитать его из исходных данных и изучать вариограмму остатков, то есть, в терминах универсального кригинга постараться найти детерминированную составляющую случайного процесса. Если же с помощью обычных полиномов этого сделать не удается, можно попробовать тригонометрические полиномы или использовать в качестве базисных функций системы ортогональных полиномов. Моделирование при наличии тренда можно выполнять с как с помощью ординарного кригинга по остаткам, прибавляя к полученному результату вычтенный ранее тренд, так и с помощью универсального кригинга, используя в качестве базисных функций дрифта те же, что и в найденном тренде. Следует отметить, что при создании цифровых моделей показателя приходится решать систему уравнений кригинга для каждого узла регулярной сетки. Кроме того, при большом количестве опорных точек (>300-500 для двойной точности) численное решение системы линейных уравнений становится неустойчивым, а при количестве в несколько тысяч и вовсе невозможным. В таких случаях прибегают к следующему приему. В уравнениях кригинга используют не все опорные точки, а только те, которые попали в заданную окрестность точки, в которой мы ищем оценку. Окрестность задается радиусом поиска (search radius) и, в принципе, может иметь эллиптическую форму в соответствии с выбранными параметрами анизотропии. Для того чтобы среди отобранных точек были представлены по возможности все направления, область поиска часто разбивают на несколько секторов (обычно 4 или 8) и константы Такой прием позволяет существенно снизить размерность решаемых систем уравнений и повысить скорость вычислений. Но здесь есть и свои проблемы. Дело в том, что при таком отборе точек моделируемая функция формально становится разрывной. Это приводит к появлению на построенной модели линий, на которых происходит заметный скачок функции, обусловленный только неравномерностью расположения точек, а не природой самого показателя. Наибольшее влияние на результат кригинга оказывает поведение модельной вариограммы вблизи начала координат. Чем круче кривая у начала координат, тем большее влияние на искомый результат оказывают ближайшие соседи (опорные точки). В итоге результирующая поверхность будет менее гладкой.
А) Б) Рис. 2.5. А) Сферическая и Б) Экспоненциальная модели вариограмм
Сферическая модель имеет 2 параметра – радиус влияния и порог, равный общей дисперсии признака. Математически сферическая модель описывает левый верхний квадрант эллипса. Экспоненциальная модель похожа на сферическую, но вблизи начала координат она восходит сначала более круто, чем сферическая, а затем, наоборот, имеет более пологий подъём и выходит на порог на расстоянии 3-х радиусов влияния.
Рис. 2.6. Модель вариограмм при разных эффектах самородков
Рис. 2.7. Интерполяция без учета анизотропии (левая часть) и с учетом анизотропии (правая часть) Основное влияние на расчеты с использованием вариограмм оказывает коэффициент радиус влияния.
На практике, стадии процесса создания вариограммной модели исследуемого объекта будут следующие: -анализ, контроль и группировка исходной информации; -построение экспериментальных вариограмм; -исследование полученных функций на наличие различных эффектов; -создание пространственной модели вариограммы.
Для реальных геологических объектов используется экспоненциальная модель, так как она более точно описывает природные процессы
|

 ).
).

 . (2.6)
. (2.6)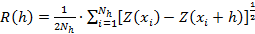 . (2.7)
. (2.7) . (2.8)
. (2.8) колеблется вблизи нуля. Если же
колеблется вблизи нуля. Если же  , то данные не подчиняются даже внутренней гипотезе, не говоря уже о более строгом условии стационарности второго порядка.
, то данные не подчиняются даже внутренней гипотезе, не говоря уже о более строгом условии стационарности второго порядка. . (2.9)
. (2.9) . (2.10)
. (2.10) стандартные отклонения для точек, находящихся соответственно в начале и в конце вектора
стандартные отклонения для точек, находящихся соответственно в начале и в конце вектора  . (2.11)
. (2.11) . (2.12)
. (2.12)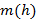 и вариограммой
и вариограммой  . Эффект пропорциональности значительно усложняет понимание результата анализа пространственного корреляционного анализа, внося в вариограмму дополнительную зависимость.
. Эффект пропорциональности значительно усложняет понимание результата анализа пространственного корреляционного анализа, внося в вариограмму дополнительную зависимость. . (2.13)
. (2.13) - локальное стандартное отклонение,
- локальное стандартное отклонение,  - локальное среднее значение.
- локальное среднее значение. ) - это подсчет описанной выше статистики, но не для всей области данных в целом, а в ее подобластях (окнах). Такой метод очень полезен для поиска зон аномальных средних значений и при наличии зон различной вариации значений (
) - это подсчет описанной выше статистики, но не для всей области данных в целом, а в ее подобластях (окнах). Такой метод очень полезен для поиска зон аномальных средних значений и при наличии зон различной вариации значений ( ).
). ):
): ):
): . (2.14)
. (2.14) . (2.15)
. (2.15)






 , тогда модельную функцию рассматривают как
, тогда модельную функцию рассматривают как .
.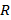 – радиус влияния или лаг (range),
– радиус влияния или лаг (range),  – эффект самородка (nugget effect),
– эффект самородка (nugget effect), – порог (sill),
– порог (sill),  - относительный эффект самородка (relative nugget).
- относительный эффект самородка (relative nugget). .
. типа модельной вариограммы при фиксированном радиусе влияния может быть сделан как визуально, путем изучения графиков выборочной и модельных вариограмм, так и автоматически с помощью метода наименьших квадратов.
типа модельной вариограммы при фиксированном радиусе влияния может быть сделан как визуально, путем изучения графиков выборочной и модельных вариограмм, так и автоматически с помощью метода наименьших квадратов. . В этом случае желательно проконтролировать найденные параметры визуально из-за возможного наличия нескольких локальных минимумов целевой функции.
. В этом случае желательно проконтролировать найденные параметры визуально из-за возможного наличия нескольких локальных минимумов целевой функции. ,
,  применяют для каждого сектора.
применяют для каждого сектора.






