Проверка статистических гипотез.
Под статической гипотезой понимают всякое предположение о распределении исследуемой случайной величины, проверяемое по выборке. Для проверки статических гипотез используют статических критерии.
Статический критерий – это правило, указывающее, когда статистическую гипотезу следует принять, а когда отвергнуть.
Критерии, относящиеся исключительно к виду функции распределения или плотности распределения исследуемой величины, называют критериями согласия.
Критерий согласия 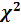
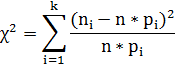
Интервалы (
| ni
| pi
| npi
| ni-npi
| (ni-npi)2
| (ni-npi)2/npi
| | 10,11
| 19,89
|
| 0,0319
| 3,1852
| 0,8148
| 0,6638
| 0,2084
| | 19,89
| 29,68
|
| 0,0795
| 7,9478
| 1,0522
| 1,1070
| 0,1393
| | 29,68
| 39,47
|
| 0,1478
| 14,7780
| 1,2220
| 1,4932
| 0,1010
| | 39,47
| 49,25
|
| 0,2048
| 20,4788
| 0,5212
| 0,2717
| 0,0133
| | 49,25
| 59,04
|
| 0,2115
| 21,1517
| -5,1517
| 26,5398
| 1,2547
| | 59,04
| 68,82
|
| 0,1628
| 16,2832
| 0,7168
| 0,5137
| 0,0316
| | 68,82
| 78,61
|
| 0,0934
| 9,3426
| 2,6574
| 7,0618
| 0,7559
| | 78,61
| 88,40
|
| 0,0399
| 3,9946
| 0,0054
| 0,0000
| 0,0000
| | 88,40
| 98,18
|
| 0,0127
| 1,2725
| -0,2725
| 0,0743
| 0,0584
| |
|
|
|
|
|
|
| 2,5625
|
Получаем наблюдаемое значение критерия: 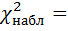 2,5625 2,5625
По таблице находим критическое значение критерия для  ;r=k-m-1=9-2-1=6 ;r=k-m-1=9-2-1=6
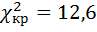
Построим график функции плотности распределения
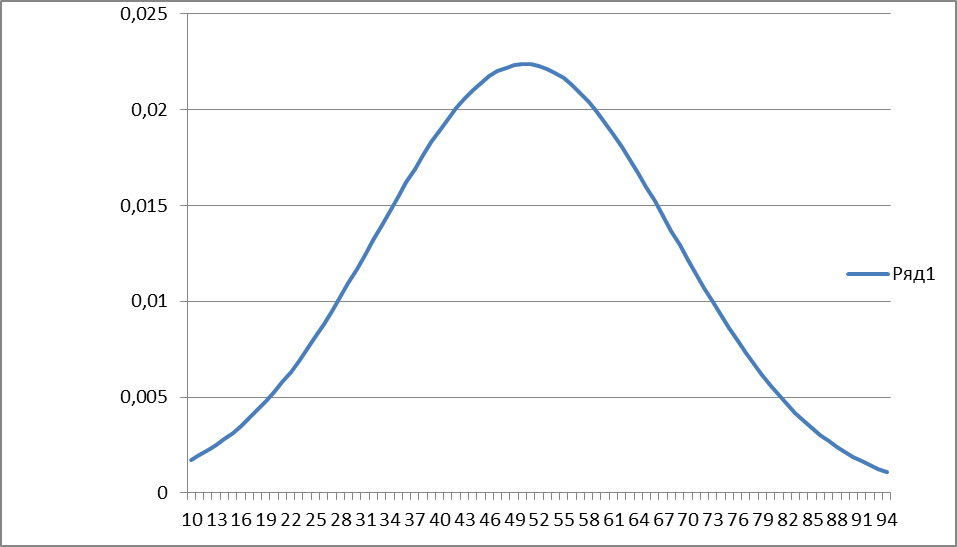
Вывод: так как  , при , при  . гипотеза не противоречит опытным данным. Также, график функции плотности вероятности по своему виду напоминает гистограмму, что является ещё одним подтверждением нормальности распределения. . гипотеза не противоречит опытным данным. Также, график функции плотности вероятности по своему виду напоминает гистограмму, что является ещё одним подтверждением нормальности распределения.
Заказать контрольную работу по статистике и не только Вы можете у нас на сайте http://otl.su
Также посетите нашу группу Вконтакте: http://vk.com/otlsu
OTL.SU – Быстро, качественно, доступно!

Практические расчеты на срез и смятие При изучении темы обратите внимание на основные расчетные предпосылки и условности расчета...
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|
Философские школы эпохи эллинизма (неоплатонизм, эпикуреизм, стоицизм, скептицизм). Эпоха эллинизма со времени походов Александра Македонского, в результате которых была образована гигантская империя от Индии на востоке до Греции и Македонии на западе...
Демографияда "Демографиялық жарылыс" дегеніміз не? Демография (грекше демос — халық) — халықтың құрылымын...
Субъективные признаки контрабанды огнестрельного оружия или его основных частей
Переходя к рассмотрению субъективной стороны контрабанды, остановимся на теоретическом понятии субъективной стороны состава преступления...
|
ТРАНСПОРТНАЯ ИММОБИЛИЗАЦИЯ
Под транспортной иммобилизацией понимают мероприятия, направленные на обеспечение покоя в поврежденном участке тела и близлежащих к нему суставах на период перевозки пострадавшего в лечебное учреждение...
Кишечный шов (Ламбера, Альберта, Шмидена, Матешука) Кишечный шов– это способ соединения кишечной стенки.
В основе кишечного шва лежит принцип футлярного строения кишечной стенки...
Принципы резекции желудка по типу Бильрот 1, Бильрот 2; операция Гофмейстера-Финстерера. Гастрэктомия Резекция желудка – удаление части желудка:
а) дистальная – удаляют 2/3 желудка б) проксимальная – удаляют 95% желудка. Показания...
|
|

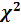
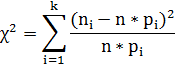

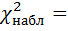 2,5625
2,5625 ;r=k-m-1=9-2-1=6
;r=k-m-1=9-2-1=6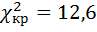

 , при
, при  . гипотеза не противоречит опытным данным. Также, график функции плотности вероятности по своему виду напоминает гистограмму, что является ещё одним подтверждением нормальности распределения.
. гипотеза не противоречит опытным данным. Также, график функции плотности вероятности по своему виду напоминает гистограмму, что является ещё одним подтверждением нормальности распределения.


