Экзаменационная программа
1. Michael W. Klein. Mathematical methods for economics. - 2nd ed. p. cm.- Addison-Wesley series in economics. 2. Багриновский К.А., Матюшок В.М. Экономико-математические методы и модели (микроэкономика). Учебное пособие. –М.: Изд-во РУДН,1999г. 3. Вавилов В.В и др. Задачи по математике. Начала анализа. – М: Наука,1990г. 4. Волкова И.О., Крутицкая Н.Н., Шагин В.Л. Математический анализ (с экономическими приложениями). – М: Изд-во ГУ-ВШЭ,1998г. 5. Гантмахер Ф.Р. Теория матриц. –М.: Наука,1988г. 6. Грес П.В. Математика для гуманитариев: Учебное пособие. – М.: Юрайт, 2000г.
7. Демидович Б. П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1997. 8. Замков О.О., Черемных Ю.Н., Толстопятенко А.В. Математические методы в экономике: Учебник - М.: "Дело и Сервис",1997г. 9. Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник. – М.: Физматлит, 2000. 10. Ивашов-Мусатов О.С. Основы математического анализа. –М.: Наука,1988г. 11. Карпелевич Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – М.:Физматгиз,1963г. 12. Кук Д., Бейз Д. Компьютерная математика. –М.: Наука,1990г. 13. Курбатов В.И., Угольницкий Г.А. Математические методы социальных технологий. Учебное пособие. –М.: Вузовская книга,1998г. 14. Курош А.Г. Курс высшей алгебры. –М.: Гостехиздат,1985г. 15. Кустов Ю.А., Юмагулов М.Г. Математика. Основы математического анализа: теория, примеры, задачи. Домашний репетитор для студентов. – М.: Рольф, Айрис-пресс, 1998. 16. Мальцев А.И. Основы линейной алгебры. –М.: Наука,1970г. 17. Мангейм Дж.Б., Рич Р.К. Политология. Методы исследования. –М.: "Весь мир",1999г. 18. Письменный Д.Т. Высшая математика. 100 экзаменационных ответов.1 курс. Домашний репетитор для студентов –М.: Рольф,Айрис-пресс,1999г. 19. Проскуряков И.В. Сборник задач по линейной алгебре. – М.: Лаборатория Базовых Знаний, 2000. 20. Столл Р. Множества, логика, аксиоматические теории. –М.: "Просвещение",1968г. 21. Томас Р. Количественные методы анализа хозяйственной деятельности. –М.: "Дело и Сервис",1999г. 22. Шипачев В.С. Математический анализ. Учебное пособие для вузов. –М.: Высшая школа,1999г.
ВЫСШАЯ МАТЕМАТИКА ИББ 1 семестр, 2012/2013 уч. год Лектор Бободжанов А.А. Экзаменационная программа
1. Определение предела в точке и при 2. Бесконечно малые функции, эквивалентные бесконечно малые функции. Бесконечно большие функции. Правило Лопиталя. 3. Непрерывные функции. Классификация точек разрыва, нахождение асимптот. 4. Определение производной. Геометрический смысл производной. Касательная к графику функции. 5. Предел, непрерывность и производная сложной функции. Логарифмическая производная. 6. Определение дифференцируемости функции. Дифференциал функции. Правила дифференцирования. Таблица производных. 7. Понятие производной и дифференциала n -го порядка. Правила вычисления производных n -го порядка. Формула Лейбница. Вычисление производных n -го порядка для табличных функций. 8. Формула Тейлора с остаточным членом в форме Лагранжа и Пеано. Формула Тейлора для элементарных функций. Приближенные вычисления значений функций. 9. Монотонность и выпуклость функции. Точки экстремума, точки перегиба. Свойства дифференцируемой функции (критерии монотонности, выпуклости, существования точек экстремума и точек перегиба). 10. Теоремы о свойствах непрерывных функций на отрезке. Формула конечных приращений Лагранжа. 11. Первообразная и неопределенный интеграл. Таблица интегралов. Замена переменных и интегрирование по частям в неопределенном интеграле. 12. Понятие определенного интеграла. Его геометрический и физический смысл. Теорема о среднем. 13. Интеграл с переменным верхним пределом. Формула Ньютона-Лейбница. Замена переменных и интегрирование по частям в определенном интеграле. 14. Несобственные интегралы первого рода. Их геометрический смысл и свойства. 15. Приложения определенного и несобственного интегралов, вычисление площадей и длин дуг. 16. Геометрические векторы. Линейные операции. Скалярное произведение векторов. Его свойства и применение. 17. Векторное и смешанное произведение векторов. Их свойства и применение. 18. Плоскость в пространстве. 19. Прямая в пространстве.
20. Матрицы. Частные типы матриц. Операции над матрицами. 21. Определитель n -го порядка. Свойства определителей. 22. Система n линейных алгебраических уравнений с n неизвестными. Правило Крамера. 23. Приведение матрицы к ступенчатому виду (метод Гаусса). Ранг матрицы. 24. Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Структура общего решения. Условие нетривиальной совместности. 25. Неоднородные системы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Структура общего решения. 26. Линейное пространство. Линейная зависимость системы векторов. Размерность, базис. Линейное подпространство. Примеры. 27. Линейный оператор, его матрица в данном базисе. Образ и ядро оператора. 28. Изменение координат вектора и матрицы оператора при переходе к новому базису. Привести примеры. 29. Собственные значения и собственные векторы линейного оператора. 30. Канонические уравнения кривых и поверхностей второго порядка (с изображениями). 31. Теоремы Ролля, Лагранжа и Коши.
|

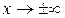 . Односторонние пределы. Действия с пределами.
. Односторонние пределы. Действия с пределами.


