ПО ЛИНЕЙНОЙ АЛГЕБРЕ И АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ
1. Даны точки А (1,–2,3), В (–1,0,3), С (5,0,–1), О (0,0,0). Найти: а) объем пирамиды построенной на векторах б) уравнение прямой, содержащей ребро в) площадь грани с ребрами г) расстояние от точки O до грани с ребрами д) уравнение прямой, содержащей высоту пирамиды, опущенной из точки е) уравнение плоскости, проходящей через точку ж) точку пересечения высоты, проведенной из точки з) уравнение перпендикуляра, проведенного к грани и) уравнение плоскости, проходящей через вершину к) уравнения плоскости, проходящей через вершины грани л) объем пирамиды, отсекаемой от пирамиды м) расстояние от основания высоты, проведенной из вершины н) угол между гранями о) угол между ребрами п) объем пирамиды, отсекаемой от пирамиды
2. Дана матрица а) решить систему б) решить систему в) решить систему г) решить систему д) решить систему ж) найти базис пространства решений системы з) найти какую-нибудь фундаментальную систему решений для системы 3. Дан оператор в пространстве R3, действующий следующим образом:
а) Найти его ранг; б) найти его собственные значения и собственные векторы; в) найти образ вектора г) найти образы базисных векторов е 1, е 2, е 3 и матрицу А е в базисе е; д) найти матрицу Аf оператора А в базисе е) найти матрицу ж) найти ранг оператора
|

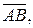

 ;
; ;
; и
и  ;
;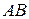 и
и  ;
; и
и  ;
; через точку пересечения медиан
через точку пересечения медиан 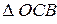 ;
; параллельно грани
параллельно грани  ;
;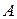 и
и 
 плоскостью, проходящей через середины ребер
плоскостью, проходящей через середины ребер 
 и
и  ;
; ;
; и
и  ;
; плоскостью, проходящей через середину ребра
плоскостью, проходящей через середину ребра  .
.

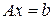 при
при 

 , где
, где 
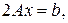 , где
, где 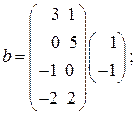


 в базисе е 1, е 2, е 3.
в базисе е 1, е 2, е 3.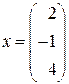 ;
;
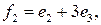
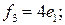
 обратного оператора А -1 в базисе е;
обратного оператора А -1 в базисе е; где
где  .
.


