Вариация альтернативного признака
Альтернативные признаки – два противоположных, взаимоисключающих друг друга качественных признака, которыми одни единицы совокупности обладают (значение варианта 1), а другие не обладают (значение варианта 0) (например, пол – мужской и женский, население – городское и сельское, продукция – годная и бракованная). Частостью (p) является доля единиц, обладающих данным признаком, в общей численности совокупности и (q = 1 – p) – доля единиц, не обладающих данным признаком, в общей численности совокупности.
Средняя арифметическая альтернативного признака
Дисперсия альтернативного признака
т.е. дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком, и доли единиц, не обладающих этим признаком. Исходя из того, что p + q = 1:
Вариацию между группами за счет признака-фактора, положенного в основу группировки, отражает межгрупповая дисперсия, которая исчисляется как средний квадрат отклонений групповой средней от общей средней:
Межгрупповая дисперсия характеризует систематическую вариацию результативного признака, т.е. вариацию между группами за счет признака-фактора, положенного в основу группировки.Вариацию внутри каждой группы изучаемой совокупности отражает внутригрупповая дисперсия, которая исчисляется как средний квадрат отклонений значений признака х от частной средней
Для всей совокупности внутригрупповую вариацию будет выражать средняя из внутригрупповых дисперсий, которая рассчитывается как средняя арифметическая из внутригрупповых дисперсий:
Внутригрупповая дисперсия отражает случайную вариацию, т.е. часть вариации обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основу группировки.Между представленными видами дисперсий существует определенное соотношение, которое известно как правило сложения дисперсий:
Правило сложения дисперсий позволяет выявить зависимость результатов от определяющих факторов с помощью соотношения межгрупповой и общей дисперсий. Это соотношение называется эмпирическим коэффициентом детерминации (η2) и показывает долю вариации результативного признака под влиянием факторного.
Эмпирическое корреляционное отношение (η) показывает тесноту связи между исследуемым явлением и группировочным признаком.
η2 и η Если связь отсутствует, то h = 0. В этом случае межгрупповая дисперсия равна нулю (δ2=0), т.е. все групповые средние равны между собой и межгрупповой вариации нет. Это означает, что группировочный признак не влияет на вариацию исследуемого признака х. Если связь функциональная, то h = 1. В этом случае дисперсия групповых средних равна общей дисперсии (
Таблица 2. - Качественная оценка связи между признаками (шкала Чэддока)
Пример 1. Определим групповые дисперсии, среднюю из групповых дисперсий, межгрупповую дисперсию, общую дисперсию по данным о производительности труда в двух бригадах:
Промежуточные расчеты занесем в таблицы:
Средняя производительность труда для 1-й бригады:
Средняя производительность труда для 2-й бригады:
Средняя производительность труда для 1-й и 2-й бригады:
Эмпирический коэффициент детерминации:
Отсюда можно сделать вывод, что общая вариация производительности труда на 45,7% обусловлена вариацией между группами. Эмпирическое корреляционное отношение
Значение h = 0,6757 показывает заметную связь по шкале Чэддока (см. таблицу 2.3) между исследуемым явлением (производительностью труда) и группировочным признаком (бригады).
|

 . (2.18)
. (2.18)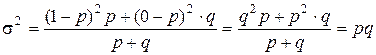 , (2.19)
, (2.19)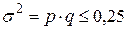 ;
;  . (2.20)
. (2.20) . (2.25)
. (2.25) :
: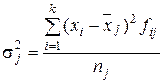 или
или  . (2.26)
. (2.26)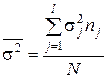 . (2.27)
. (2.27)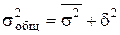 . (2.28)
. (2.28)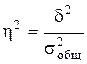 . (2.29)
. (2.29)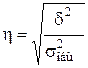 . (2.30)
. (2.30) [0, 1]. (2.31)
[0, 1]. (2.31)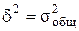 ). Это означает, что группировочный признак полностью определяет характер изменения изучаемого признака.Чем больше значение корреляционного отношения приближается к единице, тем полнее (сильнее) корреляционная связь между признаками (таблица 2.3).
). Это означает, что группировочный признак полностью определяет характер изменения изучаемого признака.Чем больше значение корреляционного отношения приближается к единице, тем полнее (сильнее) корреляционная связь между признаками (таблица 2.3).
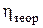
 )
)
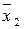 )
)
 )
)
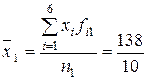 = 13,8 шт./ч.
= 13,8 шт./ч.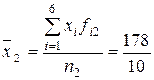 = 17,8 шт./ч.
= 17,8 шт./ч.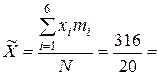
 = 15,8 шт./ч.
= 15,8 шт./ч.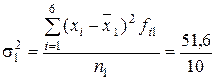 = 5,16
= 5,16
 = 4,36
= 4,36
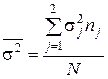 = 4,76
= 4,76
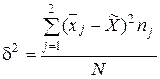 = 4,0
= 4,0
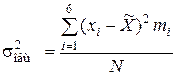 =8,76
=8,76
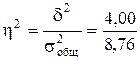 = 0,457 = 45,7%.
= 0,457 = 45,7%.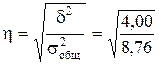 = 0,6757.
= 0,6757.


