Средние структурные величины

 

Медиана (Ме) – это вариант, который находится а середине вариационного ряда. Медиана делит ряд на две равные (по числу наблюдений) части. В ранжированных рядах не сгруппированных данных нахождение медианы сводится к отысканию порядкового номера и значения варианта у этого номера.

Медиана в интервальных вариационных рядах рассчитывается по формуле:

, (1.17)

где х ₀ – нижняя граница медианного интервала (накопленная частота которого превышает половину общей суммы частот);

– величина медианного интервала;

– накопленная частота интервала, предшествующего медианному;

– частота медианного интервала.

Также в интервальных вариационных рядах медиана может быть найдена с помощью кумуляты как значение признака, для которого

или . (1.18)

Главное свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины: .

Модой (Мо) вариационного ряда называется вариант, которому соответствует наибольшая частота.

Для вычисления моды в интервальном ряду:

, (1.19)

где х_о – нижняя граница модального интервала;

– величина модального интервала;

, , – частота n_i (в интервальном ряду с равными интервалами) или плотность распределения n_i / h_i (в интервальном ряду с неравными интервалами) модального, до и послемодального интервала.

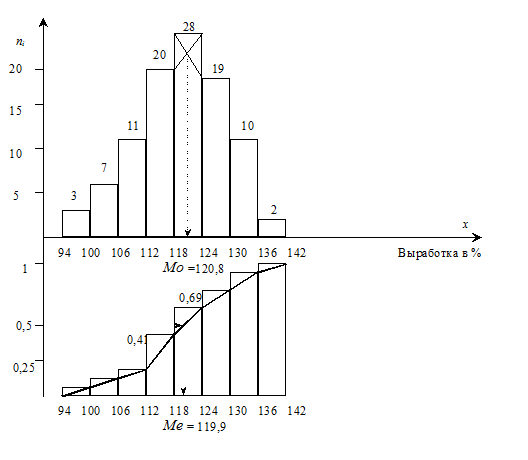
Графически отобразить моду по гистограмме можно следующим образом: нужно взять столбец, имеющий наибольшую высоту, и из его левого верхнего угла провести отрезок в угол последующего столбца, а из правого угла – в верхний правый угол предыдущего столбца, абсцисса точки пересечения отрезков и будет соответствовать модальному значению признака в изучаемой совокупности. Медиану приближенно можно определить графически - по кумуляте. Для этого высоту наибольшей ординаты, которая соответствует общей численности совокупности, делят пополам. Через полученную точку проводят прямую, параллельную оси абсцисс, до пересечения ее с кумулятой. Абсцисса точки пересечения и есть медиана (рисунок 1.1)

Рис. 1.1 Графическое отображение интервального вариационного ряда