Тесты по математике для студентов 1-го курса студентов экономического и финансово-экономического факультетов.
Тесты по математике для студентов 1-го курса студентов экономического и финансово-экономического факультетов.
I: S: Значение функции f(x) = +: -6 -: 9 -: -9 -: 50 I: S: Значение функции f(x) = -: 2 +: -: -3 -: 0 I: S: Значение функции f(x) =sin4х в точке х +: 0 -: 1 -:-1 -: 2
I: S: Значение функции f(х) =ctgх в точке х +: 0 -: 1 -:-1 -: ∞
I: S: Значение функции f(х) =ctg3х в точке х -: 0 +: 1 -:-1 -: ∞
I: S: Значение функции f(х) =tgх в точке х -: 0 -: 1 -: +: ∞
I: S: Значение функции f(х) =tg2х в точке х +: -: 1 -: -: ∞
I: S: Значение функции f(х) =tgх в точке х = -: -: 1 +: -: ∞ I: S: Значение функции f(x) =cos3x в точке х -: -: 1 -: -3 +:
I: S: Значение функции f(x)=
+: 1 -: 0 -: e -: 2
I: S: Значение функции f(x)=
-: 1 -: 0 +: e -: 2 I: S: Для какой из следующих пар множеств имеет место соотношение -: А = {a,b,c,d}; В = {a,c,d} -: А ={ b,d}; В ={a,b,c,} +: А ={a,b,d}; В = {a,b,c,d} -: A ={a,b,d} В ={a,c,d}
I: S: Указать пересечение множеств А={-3,1,2,3,4,5}, В ={3,4,6,7,-5} -: {3,4,5} -: {4,5} -: {3,5} +: {3,4}
I: S: Указать объединение множеств А ={0,1,2,3,4,5}, В ={3,4,5,6} -: {3,4,5} -: {4,5} -: {3,5,0,1,2,6,4,7} +: {0,1,2,3,4,5,6}
I: S: Указать разность множеств А ={0,1,2,3,4,5}, В ={3,4,5,6} (А\В) -: {3,4,5} -: {4,5} -: {3,5} +: {0,1,2}
I: S: Даны множества А ={0,1,2,3,4,5}, В ={3,4,5,6}, С ={-3,0,3} тогда (А ∩ В) \ С есть множество -: {3,4,5} +: {4,5} -: {3,5} -: {3,4}
I: S: Даны множества А ={0,1,2,3,4,5}, В ={3,4,5,6}, С ={-3,0,3} тогда (А U В) \ С есть множество -: {1,2,3,6} -: {4,5,6} +: {1,2,4,5,6} -: {1,2}
I: S: Даны множества А ={0,1,2,3,4,5}, В ={3,4,5,6}, С ={-3,0,3} тогда А\ (В U С) есть множество -: {1,2,3,6} -: {4,5,6} -: {1,2,4,5,6} +: {1,2}
I: S: Даны множества А ={0,1,2,3,4,5}, В ={3,4,5,6}, С ={-3,0,3} тогда А \ (В ∩ С) есть множество -: {1,2,3,6} +: {0,1,2,4,5} -: {1,2,4,5,6} -: {1,2}
I: № 1 S: Для какой из следующих пар множеств имеет место соотношение -: А = {a,b,c,d}; В = {a,c,d} +: А = {e,d}; В = {d,e} -: А = {a,b,c,d}; В = {a,d,b} -: A = {a,b,d}; В = {a,c,b}
I: S: Указать пересечение множеств А = (-1,3,-5,7); В = {3,4,5,6,7} -: {3,4,5} -: {4,5} +: {3,7} -: {3,4,}
I: S: Указать объединение множеств А = (-1,3,-5,7); В = {3,4,5,6,7} +: {-1,3,4,5,-5,6,7} -: {4,5} -: {3,5} -: {0,1,2,3,4,5,6,}
I: S: Указать разность множеств А = (-1,3,-5,7); В = {3,4,5,6,7}(A\B) -: {3,4,5} +: {-1,-5} -: {3,5} -: {0,1,2}
I: S: Если -: 1, 2, 4, 8, … +: 4, 8, 16, 32, … -: 2, 4, 8, 16, … -: 0, 2, 4, 8, …
I: S: Последовательность { +: сходящейся -: расходящейся -: возрастающей -: неограниченной
I: S: Говорят, что на множестве Х задана функция, если -: каждому х Є X ставится в соответствие не одно значение y Є Y +: каждому х Є X поставлено в соответствие одно и только одно y Є Y -: любому х Є X ставится в соответствие любое y Є Y -: каждому х Є X по некоторому правилу или закону ставится в соответствие несколько значений y Є Y
I: S: Множество Х, на котором задана функция, называется -: функцией одной переменой -: графиком функции y = f (x) -: множеством значений функции f и обозначается E(f) +: областью определения функции f и обозначается D(f)
I: S: К способам задания функций не относится +: дидактический способ -: аналитический способ -: графический способ -: табличный способ
I: S: Пусть заданы прямоугольная система Oxy и функция y = f (x). Графиком функции f (x) называется -: множество значений функции f (x) +: множество всех точек плоскости с координатами (x; f (x)), где х Є D(f) -: область определения функции f (x) -: множество всех х Є X
I: S: Значение функции f(x) =sin2х в точке х +: 0 -: 1 -:-1 -: 2
I: S: Значение функции f(x) =cos6x в точке х -: -: 1 +: 0 -: I: S: Значение функции f(x) =cos4x в точке х +: -: 1 -: 0 -: I: S: Значение функции f(x) =sin2х в точке х -: 0 +: -:-1 -: 2
I: S: Значение функции f(x) =cos2x в точке х -: -: 1 +: -: I: S: Значение функции f(x) =cos4x в точке х -: -: 1 -: +:
I: S:
-: +: -: 2 -:
I: S:
-: 1 -: 2 -: +:
I: S:
-: 1 -: +: -: 2
I: S:
-: 2 -: -: 3 +:
I: S:
-: 1 -: 2 -: +:
I: S:
-: -: 2 -: 1 +: -1
I: S:
-:
-:
+:
-: 3
I: S:
-: 1 +: 0 -: 2 -:
I: S:
-: 0 -: 1 -: 2 +:
I: S:
+: 0 -: 1 -: 2 -:
I: S:
-: 1 -: 2 -: +: 0
I: S:
Для задания функции существуют следующие способы: аналитический,........, графический. Какой способ пропущен? -: логический +: табличный -: абстрактный -: неявный
I: S: Совокупность всех значений аргумента -: областью значений этой функции -: областью переменных значений -: областью значений аргумента +: областью определения этой функции
I: S: Совокупность всех значений, принимаемых переменной -: областью определения этой функции -: областью переменных значений +: областью значений этой функции -: совокупной областью
I: S:
-: показательной функцией -: логарифмической функцией -: обратной функцией +:степенной функцией
I: S: Какая функция является четной? -:
+:
-:
-:
I: S:
-:
-:
-:
+:
I: S:
-:
-:
+:
-:
I: S:
-:
-:
-:
+:
I: S:
-:
+:
-:
-:
I: S:
+:
-:
-:
-:
I: S:
+:
-:
-:
-:
I: S:
-:
+:
-:
-:
I: S:
+:
-:
-:
-:
I: S:
-:
-:
+:
-:
I: S:
+:
-:
-:
-:
I: S:
-:
-:
-:
+:
I: S:
+:
-:
-:
-:
I: S:
-: 0 -: ½ +: 1 -: 1/4
I: S: Числовую последовательность называют сходящейся, если... -: ее предел равен "нулю" +: она имеет предел -: ее предел равен "бесконечности" -: она не имеет предела
I: S:
+:
-:
-:
-:
I: S:
-:
+:
-:
-:
I: S:
-: переменной «х» -: значению «Х0» +: величине «А» -: нулю «0»
I: S:
+:
-:
-:
-:
I: S:
-:
-:
+:
-:
I: S:
-:
-:
+:
-:
I: S: Для нахождения предела элементарной функции необходимо... -: разделить ее на предельное значение аргумента -: приравнять ее любому значению аргумента -: приравнять ее предельному значению аргумента +: подставить в нее предельное значение аргумента
I: S:
-: эта функция не имеет предела +: для нахождения предела необходимо преобразовать эту функцию -: неверно указано предельное значение аргумента -: надо изменить предельное значение аргумента
I: S:
-: " 0 " (нулю) -: " 1 " (единице) +: бесконечности -: величине " С "
I: S: Число Эйлера является основанием натурального логарифма. Чему оно приближенно равно? -: 3,142 -: 2,54 -: 3,62 +: 2,718
I: S: Предел частного двух функций равен +:
-:
-:
-: 0
I: S:
-: бесконечности +: " 0 " (нулю) -: " 1 " (единице) -: величине " С "
I: S:
-: " 0 " (нулю) -: " e " (основанию натурального логарифма) -: бесконечности +: " 1 " (единице)
I: S:
-: " 0 " (нулю) -: " 1 " (единице) +: " e " (основанию натурального логарифма) -: бесконечности
I: S: Первый замечательный предел имеет вид: +:
-:
-:
-:
I: S:
-: " 0 " (нулю) -: " 1 " (единице) +: " e " (основанию натурального логарифма) -: бесконечности
I: S:
+:
-:
-:
-:
-: Разделить числитель и знаменатель на 2 -: Умножить числитель и знаменатель на (х-1) -: Извлечь квадратный корень из числителя и знаменателя +: Разложить числитель на множители и сократить дробь на (х-1)
I: S:
+:
-:
-:
-:
I: S: Уравнение +: прямую, параллельную оси ординат -: прямую, параллельную оси абсцисс -: прямую, совпадающую с осью ординат -: прямую, совпадающую с осью абсцисс
I: S: Уравнение -: прямую, параллельную оси ординат -: прямую, параллельную оси абсцисс +: прямую, совпадающую с осью ординат -: прямую, совпадающую с осью абсцисс
I: S: Уравнение -: прямую, параллельную оси ординат -: прямую, параллельную оси абсцисс -: прямую, совпадающую с осью ординат +: прямую, совпадающую с осью абсцисс
I: S: Уравнение -: прямую, параллельную оси ординат +: прямую, параллельную оси абсцисс -: прямую, совпадающую с осью ординат -: прямую, совпадающую с осью абсцисс
I: S:
Значение предела -: -: +: -:
I: S: Значение предела
-:
+: -:
-:
I: S: Значение предела
+:
-:
-:
-:
I: S: Значение предела -:
-:
+:
-:
I: S: Значение предела -:
-:
+:
-:
I: S: Значение предела -: +: -: -:
I: S: Указать формулу общего члена последовательности -: (n+1)/n2 -: n2+2n+3 +: (n+1)/n -: 1/n2
I: S: Какая из последовательностей { x n} ограничена сверху -: 2, 4, 6, 8, … +: 1, –4, –9, –16, … -: 1, 3, –5, 7, … -: 2, 4, –8, 16, …
I: S: Какая из последовательностей { x n} ограничена снизу +: 2, 4, 6, 8, … -: 1, –4, –9, –16, … -: 1, 3, –5, 7, … -: 2, 4, –8, 16, …
I: S: Какая из последовательностей { x n} ограничена: -: 2,4,6,8, … -: 1, –4, –9, –16, … +: 1/3, 1/32, 1/33, … -: 2, 4, –8, 16, …
I: S: Какая из последовательностей { x n} является возрастающей: -: x n = (-1)n/ n -: x n =1/n2 -: x n = ─√ n +: x n = 2n + 1
I: S: Предел последовательности -: 1/2 +: 0 -: 2 -: 1/5
I: S: Предел последовательности -: 1/2 -: 2 -: 2 +: -1/2
I: S: Предел последовательности -: 1/2 -: 2 +: ∞ -: -1/2
I: S: Найти (f (b) – f (a)) / (b – a), если f (x) = x 2: -: 1 +: а + b -: а – b -: 2 а – b
I: S: Для функции f (x) = (x + 3)/(x 2 – 1); найти f (0): -: 1 -: 3 +: -3 -: -1
I: S: Минимальное значение функции f (x) = 1 + x 2 равно -: 4 -: 2 -: 0 +: 1
I: S: Максимальное значение функции f (x) = 1 – x 2 равно -: 4 -: 2 +: 1 -: 0
I: S: Областью определения функции y = ln (x + 2) является -: [-5,1] -: [3,+∞] +: (-2,+∞) -: [2,3]
I: S: Областью определения функции f (x) = (3 x + 1)/(x 2 + 1) является -: [-5,1] +: (-∞,+∞) -: [1,+∞) -: [2,3]
I: S: Найти область определения функции f (x) = 21/x
-: [-5,1] +: (-∞,0) U (0 + ∞) -: (1,+ ∞) -: [2,3]
I: S: Найти область определения функции y = arcsin ((x + 2)/3) +: х Є [-5,1] -: х Є (-∞,-5) -: х Є [1,+∞) -: х Є [2,3]
I: S: Найти множество значений функции y = 3 - 5cos x -: E (f) = (2,∞) -: E (f) = [5,8] -: E (f) = [-2,-8] +: E (f) = [-2,8]
I: S: Функция называется четной, если +: f (- x) = f (x) -: f (- x) = - f (x) -: f (x +T) = f (x) -: f (x - T) = f (x)
I: S: Функция называется нечетной, если -: f (- x) = f (x) +: f (- x) =- f (x) -: f (x + T) = f (x) -: f (x - T) = f (x)
I: S: График четной функции симметричен относительно +: оси OY -: оси OX -: начала координат -: не симметричен
I: S: График нечетной функции симметричен относительно -: оси OY -: оси OX +: начала координат -: не симметричен
I: S: Какая из следующих функций является четной? -: y = x 3/(x 2 +1) +: y = x 4 – 5| x | -: y = e x – 2 e -x -: y = (1 – x)/(1 + x)
I: S: Какая из следующих функций является нечетной? -: y = | x | + 2 -: y = sin x + 1 +: y = x 2n sin x -: y = sin x - 1
I: S: Какая из следующих функций является функцией общего вида (не является ни четной, ни нечетной)? -: y = x 5 + 3 x 3 - x -: y = | x | - 2 +: y = -: y = arcsin x
I: S: Бесконечно малые функции -: -: -: +:
I: S: Значение предела -: 10 -: 5 -: –5 +: –10
I: S: Значение предела -: 10 +: 0 -: –5 -: –10
I: S: Значение предела -: 10 -: 5 +: ∞ -: –10 I: S: Если f (x 2) ≥ f (x 1) при x2 > x1, то функция +: неубывающая -: убывающая -: возрастающая -: ограниченная
I: S: Если f (x 1) ≥ f (x 2) при x2 > x1, то функция -: убывающая -: возрастающая -: неубывающая +: невозрастающая
I: S: Если f (x 2) -: убывающая +: возрастающая -: ограниченная -: неубывающая
I: S: Если f (x 1) -: возрастающая -: неубывающая +: убывающая -: невозрастающая
I: S: Указать первые четыре члена последовательности, если x n = (-1)n/ n -: -1, 2, -4, 8, … -: -: 2, 4, 8, 16, … +: -1, 1/2, - 1/3, 1/4, …
I: S: Указать формулу общего члена последовательности -1,2,-3,4,-5, … +: (-1)n n -: - n 2 + 2 n + 3 -: (-1)n -: -1/ n 2
I: S: Какая из последовательностей { x n} ограничена сверху +: -2,-4,-6,-8,… -: –1, 4, – 9,16,… -: -1,3, – 5,7,… -: –2, 4, – 8,16,…
I: S: Какая из последовательностей { x n} ограничена снизу -: -2,4,-6,8,… -: –1, – 4, – 9, – 16,… +: 1,3,5,7,… -: –2, 4, – 8,16,…
I: S: Какая из последовательностей { x n} ограничена. -: 2,4,6,8,… +: -: –1, – 4, – 9, – 16,… -: –2, 4, – 8, 16, …
I: S: Для функции f (x) = x 3 2x; найти f (1) -: 1 -: 3 -: -3 +: 2
I: S: Найти минимальное значение функции f (x) = | x | - 1 -: 0 -: 2 +: -1 -: 1
I: S: Найти максимальное значение функции f (x) = 4 – x 2 -: 2 -: 1 -: -4 +: 4
I: S: Найти область определения функции y = ln (1-x2): -: х Є (-∞, -1] +: х Є (-1,1) -: х Є [1,+∞) -: х Є(-∞, +∞)
I: S: Найти область определения функции f (x) = arcos 3 x -: х Є [-5,1] +: х Є [-1/3, 1/3] -: х Є [1,+∞) -: х Є [2,3] I: S: Сумма и произведение двух бесконечно малых функций при х → х 0 являются -: бесконечно большими функциями -: ограниченными функциями +: бесконечно малыми функциями -: эквивалентными функциями
I: S: Функция f (x) в точке х 0 может иметь -: два предела -: конечное число пределов +: только один предел -: бесконечно много пределов
I: S: Найти наибольшее значение функции y = x 2 на отрезке [1, 4] -: 4 +: 16 -: 1 -: 8
I: S: Найти наименьшее значение функции y = x 3 на отрезке [1, 2] -: 8 -: 2 -: 3 +: 1 I: S: Область определения функции y = sin (x – 2) – это -: интервал (0, 2) -: отрезок [-1, 1] +: вся числовая прямая -: вся числовая прямая, кроме точки х = 2
I: S: Область определения функции y = tg (x + 1) – это -: интервал (0, 1) -: интервал (-1, 0) -: вся числовая прямая +: вся числовая прямая, за исключением точек x = ( I: S: Вычислить область определения функции y = ln (x 2 – 16) -: вся числовая прямая -: интервал (-4; 4) +: (-∞; -4) -: [4; +∞)
I: S: Область определения функции y = ln( 16 – x 2) -: вся числовая прямая +: интервал (-4; 4) -: [4; +∞) -: (-∞; -4)
I: S: Последовательность -: невозрастающая и неограниченная -: возрастающая и неограниченная +: убывающая и ограниченная -: возрастающая и ограниченная
I: S: Последовательность -: убывающая и ограниченная -: невозрастающая и ограниченная -: возрастающая и ограниченная +: возрастающая и неограниченная
I: S: Последовательность +: возрастающая и ограниченная -: убывающая и ограниченная -: невозрастающая и ограниченная -: возрастающая и неограниченная
|

 в точке х
в точке х  =2 равно
=2 равно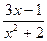 в точке х
в точке х 
 равно
равно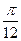 равно
равно
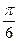 равно
равно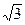

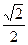
 в точке х
в точке х 
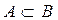
 , то первые четыре члена последовательности будут
, то первые четыре члена последовательности будут } = 1, 1/2, 1/6, 1/24, … является
} = 1, 1/2, 1/6, 1/24, … является
 равно
равно
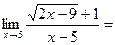












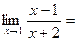




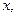 для которых функция
для которых функция  определена, называется...
определена, называется... называется...
называется...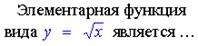



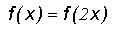







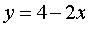




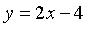




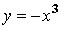








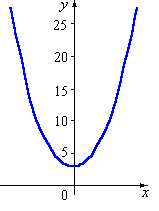



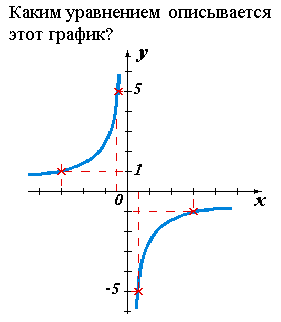







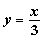






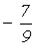

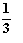




















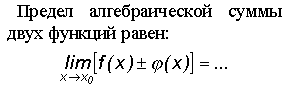

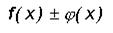


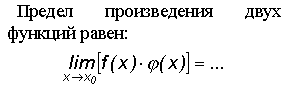



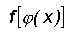




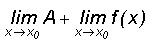





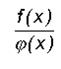
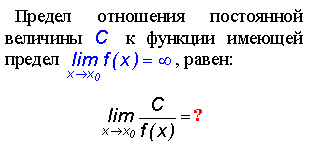
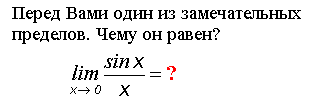

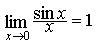
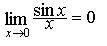



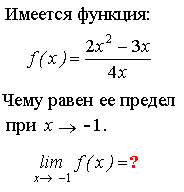

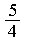







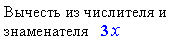

 определяет
определяет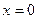 определяет
определяет определяет
определяет определяет
определяет равно
равно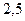



 равно
равно



 равно
равно

 равно
равно



 равно
равно
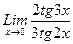 равно
равно

 , 3/2, 4/3, 5/4, …
, 3/2, 4/3, 5/4, …
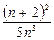 равен
равен
 равен
равен равен
равен
 и
и  называются эквивалентными, если
называются эквивалентными, если





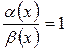

 равно
равно равно
равно равно
равно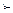 f (x 1) при x2 > x1, то функция
f (x 1) при x2 > x1, то функция , 3/2, 4/3, 5/4, …
, 3/2, 4/3, 5/4, … - 1) kπ;, k = 0, 1, 2, …
- 1) kπ;, k = 0, 1, 2, … (4; +∞)
(4; +∞)





