Кратчайший путь в орграфе

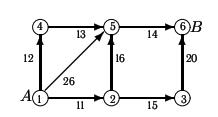
Дугам во взвешенном орграфе поставлено в соответствие некоторое число (вес). Это может быть евклидово расстояние между вершинами или какая-либо другая числовая характеристика (цена, время, энергия). Ставится задача нахождения кратчайшего пути во взвешенном орграфе от одной заданной вершины до другой. Длина пути — сумма весов дуг пути. Вес дуг может быть положительным, отрицательным, нулевым или бесконечным (что соответствует отсутствию дуги).

З а д а ч а. Для заданного орграфа найти кратчайший путь от вершины s к вершине t. На рисунке рядом с дугой указан ее вес.

 

Пр и м е р. Дан взвешенный орграф. Найти кратчайший путь из вершины A в B.

Р еше н и е. Применим алгоритм Е. Дейкстры. Пошаговый алгоритм определения кратчайшего расстояния от вершины A до B состоит в следующем. С каждой вершиной связывается метка. Метка может быть постоянной или временной. Первоначально вершине A приписывается постоянная метка 0, а всем остальным метка ∞. На первом шаге вычисляются расстояния от вершины A с постоянной меткой до всех остальных вершин. Если некоторая вершина не соединена с вершиной с постоянной меткой или дуга направлена в обратную сторону, то расстояние принимается бесконечным. Найденные расстояния являются временными метками вершин. Минимальная из временных меток берется за постоянную. На следующем шаге временные метки всех вершин (кроме тех, у которых постоянные метки) вычисляются как сумма значения последней полученной постоянной метки и расстояния от нее в случае, если это значение не больше предыдущего значения временной метки данной вершины. Таким образом, временная метка вершины может или оставаться прежней, или уменьшаться. Минимальная из временных меток всех вершин опять принимается за постоянную. Процесс продолжается до тех пор, пока вершина B не получит постоянную метку. Значение этой метки и есть кратчайшее расстояние от A до B.

Рассмотрим отдельные шаги решения.

1. Вершина A получает постоянную метку 0, остальные — метку ∞:

2. Вычисляем расстояния от вершины 1 с постоянной меткой 0. Вершины 2, 4 и 5 меняют свои временные метки на 11, 12 и 26. Остальные имеют прежние метки — ∞. Очевидно, наименьшей меткой является 11. Она и становится постоянной:

3. Вычисляем расстояния от вершины 2 с постоянной меткой 11. Вершины 3 и 5 имеют расстояния 15 и 16 до вершины 2. Суммируя, получаем значения 26 и 27. Для вершины 5 прежнее значение, 26, было меньше нового значения 27. Следовательно, значение метки 5 не меняем; оно остается равным 26. Из трех временных меток — 12, 26 и 26 — наименьшая принадлежит вершине 4. Эта метка и становится постоянной:

4. Вычисляем расстояния от вершины 4 с постоянной меткой 12. Вершина 5 имеет до нее расстояние 13. Суммируя (13+12), получаем значение 25 временной метки вершины 5 вместо прежнего значения 26. Из двух временных меток вершин 3 и 5 наименьшая принадлежит вершине 5. Эта метка и становится постоянной:

5. На следующем этапе, вычисляя расстояния от вершины 5 с постоянной меткой 25, приходим к конечной вершине B. Но ее метка (25+14 = 39) не становится постоянной, так как она не является минимальной. Расстояние от вершины 5 до вершины 3 принято ∞ (они не соединены). Прежнее значение временной метки вершины 3 меньше ∞. Поэтому метка вершины 3 не меняется. Метка вершины 3 со значением 26, меньшим 39, становится постоянной.

На следующем этапе ищем расстояния от нее:

6. Расстояние от вершины 3 до вершины 6 составляет 20. Так как 26 + 20 > 39, значение метки 6 не меняем. На этом шаге она остается прежней и единственной временной меткой. Временная метка вершины 6 становится постоянной, что означает конец процесса. Минимальное расстояние от A до B равно 39.