Поток в сети

Сетью называют взвешенный орграф с двумя выделенными вершинами: истоком и стоком. Исток имеет нулевую полустепень захода, а сток — нулевую полустепень исхода. Вес дуги означает ее пропускную способность. Поток — еще одно число, приписанное дуге. Поток дуги не больше ее пропускной способности и может меняться. Поток выходит из истока и без потерь, в том же объеме заходит в сток. Условие равновесия (по объему входа и выхода) выполняется и для каждой вершины сети.

Задача о наибольшем потоке в сети — не единственная, но, вероятно, основная задача для потоков в сети. Очевидна возможность практического применения этой задачи для решения транспортных проблем (пробки на дорогах можно условно связывать с насыщением сети или отдельной ее дуги), проблем транспортировки нефтепродуктов или электроэнергии.

 

З а д а ч а. Задана пропускная способность дуг транспортной сети с началом (истоком) в вершине s и концом (стоком) в вершине t. Используя алгоритм Форда–Фалкерсона, найти максимальный поток по сети.

 

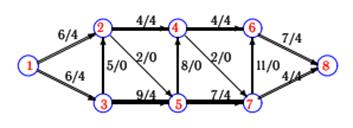
Пр и м е р. Задана пропускная способность дуг транспортной сети с началом в вершине 1 и концом в вершине 8. Используя алгоритм Форда–Фалкерсона, найти максимальный поток по сети.

Р еше н и е. Алгоритм состоит из двух частей — насыщения потока и его перераспределения. Поток называется насыщенным, если любая цепь из истока в сток содержит насыщенную дугу. В первой части алгоритма разыскиваются цепи из истока в сток и все дуги цепи насыщаются одинаковым возможно большим потоком, определяемым пропускной способностью наиболее «тонкой» дуги или наименьшей разностью между пропускной способностью и потоком в дуге. Различные цепи могут иметь общие дуги. Полученный поток согласован с условием сохранения в узлах (вершинах). Поток, входящий в вершину, равен потоку, выходящему из нее. Поток в сети проходит по цепям из истока в сток, т.е. недопустим многократный проход по отдельной дуге. Первая часть задачи считается решенной, если нет ненасыщенных цепей из истока в сток. Первая часть задачи не имеет единственного решения.

Во второй части перераспределение потока выполняется исходя из условия достижения общего по сети максимума потока. Для этого в основании графа (т.е. в графе, в котором снята ориентация дуг) разыскиваются маршруты из истока в сток, состоящие из ребер, соответствующих ненасыщенным дугам, направленным вперед, и непустым дугам, направленным назад. Потоки в дугах прямого направления увеличиваются на величину, на которую уменьшаются потоки в обратных дугах выбранного маршрута. При этом, очевидно, нельзя превышать пропускную способность дуг, направленных вперед, и допускать отрицательных потоков в обратных дугах. В некоторых случаях при удачном выборе цепей в первой части алгоритма перераспределения потока не требуется.

1. Насыщение потока. Рассмотрим путь 1–2–4–6–8. Пропустим через этот путь поток, равный 4. При этом дуги [2, 4] и [4, 6] будут насыщенными. Аналогично, путь 1–3–5–7–8 насытим потоком 4. Распределение потока отметим на графе (рис. 4.5). В числителе ставим пропускную способность, в знаменателе — поток. Числитель всегда больше знаменателя, а знаменатель может быть и нулем.

Заметим, что из 1 в 8 есть еще ненасыщенный путь, 1–3–2–5–4–7– 6–8,поток в котором можно увеличить на 2. При этом насытятся дуги [1, 3], [2, 5] и [4, 7].

Из 1 в 8 больше нет ненасыщенных путей. По дуге [1,3] двигаться нельзя (она уже насыщена), а движение по дуге [1,2] заканчивается в вершине 2, так как обе выходящие из нее дуги насыщены.

2. Перераспределение потока. Найдем последовательность вершин от 1 к 8, такую, что дуги, соединяющие соседние вершины, направленные из 1 в 8, не насыщены, а дуги, направленные в обратном направлении, не пусты. Имеем единственную последовательность: 1–2–3–5–7–6–8. Перераспределяем поток. Поток в дугах прямого направления увеличиваем на 1, а поток в дугах обратного направления уменьшаем на 1. Процесс продолжаем до тех пор, пока одна из прямых дуг не будет насыщена или какая-нибудь обратная дуга не будет пуста.

Поток в насыщенной сети можно посчитать по потоку, выходящему из истока 1 или входящему в сток 8. Очевидно, эти числа должны быть равны. Кроме того, для проверки решения следует проверить условие сохранения потока по узлам. Для каждого узла суммарный входящий поток должен быть равен выходящему. В рассматриваемом примере поток равен 11. Распределение потока по дугам при одном и том же суммарном минимальном потоке в сети не единственное.