Маршруты в орграфе
По подсчетам римских историков, в Древней Греции было 288 философских учений, из которых помимо великих философских школ выделяется учение киников и киренских философов. В Афинах существовало четыре большие школы: Академия Платона, Ликей Аристотеля, Портик (стоическая школа) и Сад (эпикурейская школа).
Натурфилософы: Фалес (все вещи возникают из воды и вновь превращаются в воду; вода – вечное начало), Анаксимен (субстрат всех вещей – воздух), Анаксимандр (апейрон – “бесконечное”– неопределенное, вечное и бесконечное, постоянно находящееся в движении первоначало)., Гераклит Эфесский - огонь–начало, субстанция бытия. Наивный материализм - эллейская школа – Парменид, Зенон, Ксенофан - дальнейший этап на пути рационализации знания. Элеаты впервые перешли от конкретных природных стихий к бытию как таковому. Стихийная диалектика - Гераклит, Кратил. Демокрит – бытие – нечто простое, далее неделимое, непроницаемое – атом. • Натурфилософы видели единое многообразие мира в его вещественной основе. Им не удалось объяснить социальные и духовные явления. • Школа Сократа–Платона развила концепцию идей, на основе которой можно было объяснять не только природу, но и человека и общество. • Аристотель развил учение о форме, что позволило лучше понять сущность отдельной вещи. Аристотель имел большое влияние на императора Александра Македонского, был его учителем. Он и его ученики предлагали законодательные системы для новых греческих городов и колоний. • Киники, стоики, эпикурейцы, скептики были заняты поисками удела, смысла жизни человека. Их общий призыв: будь мудрым.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФГБОУ ВО «Воронежский государственный университет КАФЕДРА ИНФОРМАЦИОННЫХ ТЕХНоЛОГИЙ МОДЕЛИРОВАНИЯ И УПРАВЛЕНИЯ
Методические указания и задания К контрольной работе № 2 по дисциплине “ДИСКРЕТНАЯ МАТЕМАТИКА ”
для студентов 1-го курса ФБО направления 09.03.02
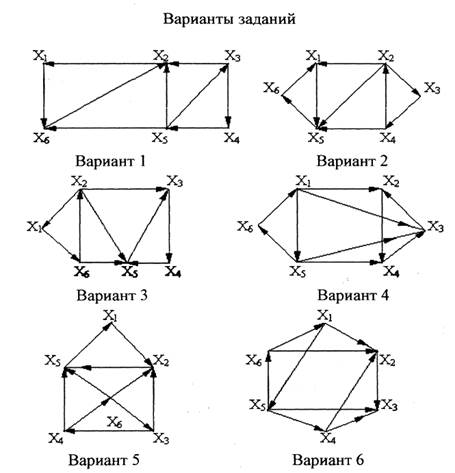
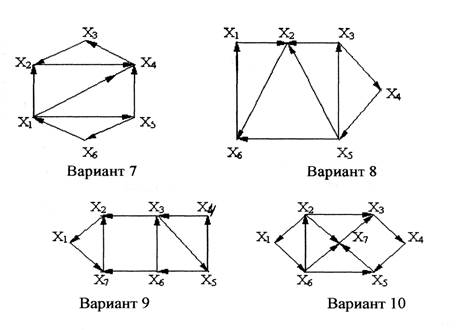
Воронеж 2014 Контрольная работа состоит из четырех заданий. К кажому заданию приведены необходимые для их выполнения теоретические сведения и примеры выполнения заданий. Ход выполнения и результаты решения заданий студентом оформляются средствами MS WORD. Номер варианта каждого задания выбирается по последней цифре шифра логина студента. Маршруты в орграфе Задачи, связанные с маршрутами в орграфе, имеют большое практическое значение, что и дает стимул к развитию и совершенствованию методов их решения. Наиболее часто встает вопрос о минимальных и максимальных расстояниях, о числе маршрутов определенной длины. Особенность таких задач для орграфов состоит в том, что несмотря на небольшой порядок графа (в приведенном ниже задании предлагается порядок 5) простое решение неочевидно. В следующей задаче для решения предлагается легко программируемый (особенно в системах компьютерной математики) алгебраический метод. Длина маршрута здесь измеряется в числе дуг, входящих в него. Допускаются замкнутые маршруты. З а д а ч а. Дан орграф порядка 6 Сколько в нем маршрутов длины 3? Записать их.
Пример. Дан орграф. Сколько в нем маршрутов длиной 3?
Решение. Используем алгебраический метод решения задачи. Запишем матрицу смежности. Матрица смежности орграфа — несимметричная:
Возведем эту матрицу в степень 3:
Суммируя все элементы полученной матрицы, находим, что число маршрутов длиной 3 равно восьми. Три единицы, стоящие по диагонали, показывают, что сюда входит 3 помеченных контура. Очевидно, это контуры 1–4–3, 4–3–1 и 3–1–4. Проверить наличие контура в орграфе можно также методом топологической сортировки. Если граф не может быть отсортирован топологически, то в нем есть контуры.
|


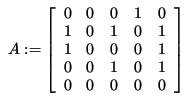
 .
.


