Вопрос №1.
1. Храмкина М.Н. Практикум по органическому синтезу.- Л.: Химия, 1988. С 267 – 273, 280 – 281. 2. Храмкина М.Н. Практикум по органическому синтезу.- М.: Химия, 1974. 3. Гороновский И.Г. Краткий справочник по химии.- К.:Наукова думка, 1974. 4. Потапов В.М., Татаринчик С.Н. Органическая химия. М.: Химия,1980. 5. Аверина А.В. Лабораторный практикум по органической химии.- М.: Высш.шк., 1980. 6. Березан О.М. Органічна хімія.- К.: Абрис, 2000. 7. Липатников В.Е. Лабораторные работы по неорганической и органической химии.- М.: Высш.шк., 1981.
Витрачено робочих годин __________________ Препарат здано_____________________________ Відмітка про здачу речовини Підпис викладача Самарский финансово-экономический колледж (Самарский филиал Финуниверситета)
КОМПЛЕКТ ЛЕКЦИЙ по дисциплине «Статистика» по специальностям 080114 «Экономика и бухгалтерский учёт» (по отраслям) (базовая и углубленная подготовка), 38.02.01«Экономика и бухгалтерский учёт» (по отраслям), (базовая подготовка), 38.02.06 «Финансы», (базовая подготовка), 38.02.07 «Банковское дело» (базовая подготовка)
Составлен Преподавателем Н.А.Свидерской
Самара
Урок №10 Тема 6.2. Методы анализа основной тенденции в рядах динамики, анализ сезонных колебаний. План Выявление основной тенденции динамического ряда. Экстраполяция тенденции как метод прогнозирования. Сезонные колебания. Вопрос №1. Одной из важнейших задач статистики является определение в рядах динамики общей тенденции развития явления. На развитие явления во времени оказывают влияние факторы, различные по характеру и силе воздействия. Одни из них оказывают практически постоянное воздействие и формируют в рядах динамики определенную тенденцию развития. Воздействие же других факторов может быть кратковременным или носить случайный характер. Основная тенденция (тренд) – изменение, определяющее общее направление развития, это систематическая составляющая долговременного действия. Задача – выявить общую тенденцию в изменении уровней ряда, освобожденную от действия различных случайных факторов. Методы выявления тренда: 1) Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда динамики (одновременно уменьшается количество интервалов). Средняя, исчисленная по укрупненным интервалам, позволяет выявить направление и характер (ускорение или замедление роста) основной тенденции развития, в то время как слишком малые интервалы между наблюдениями приводят к появлению ненужных деталей в динамике процесса, засоряющих общую тенденцию.
Различные направления изменений уровней ряда по отдельным месяцам затрудняют выводы об основной тенденции производства. Если соответствующие месячные уровни объединить в квартальные и вычислить среднемесячный выпуск продукции по кварталам, т.е. укрупнить интервалы, то решение задачи упрощается.
После укрупнения интервалов основная тенденция роста производства стала очевидной: 5,23<5,57<5,87<6,03 млн.руб. 2) Метод скользящей среднейзаключается в том, что исчисляется средней уровень из определенного числа (обычно нечетного) первых по счету уровней ряда, затем – из такого же числа уровней, но начиная со второго по счету, далее – начиная с третьего и т.д. Таким образом, средняя как бы “скользит” по ряду динамики, передвигаясь на один срок. Недостатком сглаживания ряда является укорачивание сглаженного ряда по сравнению с фактическим, а, следовательно, потеря информации.
Сглаженный ряд урожайности по трехлетиям короче фактического на один член ряда в начале и в конце, по пятилетиям – на два члена в начале и в конце ряда. Он меньше, чем фактический, подвержен колебаниям из-за случайных причин, и четче выражает основную тенденцию роста урожайности за изучаемый период, связанную с действием долговременно существующих причин и условий развития. Укрупнение интервалов и метод скользящей средней дают возможность определить лишь общую тенденцию развития явления, более или менее освобожденную от случайных или волнообразных колебаний. Получить обобщенную статистическую модель тренда посредством этих методов нельзя.
3) Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда динамики во времени. Определение теоретических (расчетных) уровней ŷt производится на основе так называемой адекватной математической модели, которая наилучшим образом отображает (аппроксимирует) основную тенденцию ряда динамики. Простейшими моделями, выражающими тенденцию развития, являются (где a 0, a 1 – параметры уравнения; t – время): ŷt = a 0 + a 1· t. Расчет параметров функции обычно производится методом наименьших квадратов. Выравнивание ряда динамики заключается в замене фактических уровней yi плавно изменяющимися уровнями ŷt, наилучшим образом аппроксимирующими статистические данные. Выравнивание по прямой используется в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии. Выравнивание по показательной функции используется в тех случаях, когда ряд отражает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны. Выравнивание ряда динамики по прямой ŷt = a 0 + a 1· t. Параметры a 0, a 1 согласно МНК находятся решением следующей системы нормальных уравнений:
где y – фактические (эмпирические) уровни ряда; t – время (порядковый номер периода или момента времени). S t = 0, так что система нормальных уравнений принимает вид:
Отсюда можно выразить коэффициенты регрессии:
Если расчеты выполнены правильно, то S y = S ŷt.
|



 ;
;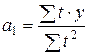 .
.


