Внутренняя энергия идеального газа
Внутренней энергией тела называют часть его полной энергии за вычетом кинетической энергии движения тела как целого и потенциальной энергии тела во внешнем поле. Таким образом, во внутреннюю энергию входят кинетическая энергия поступательного и вращательного движений молекул, потенциальная энергия их взаимодействия, энергия колебательного движения атомов в молекулах, а также энергия различных видов движения частиц в атомах. В идеальном газе потенциальная энергия взаимодействия молекул пренебрежимо мала и внутренняя энергия равна сумме энергий отдельных молекул
где Ei — энергия отдельной молекулы. До сих пор мы пользовались представлением о молекулах как о материальных точках. Кинетическая энергия молекул считалась совпадающей с энергией их поступательного движения, а средняя кинетическая энергия молекулы полагалась равной Ввиду полной беспорядочности движения молекул в газе все направления перемещения молекулы равновероятны. Поэтому на каждую степень свободы поступательного движения приходится в среднем энергия
Представление о молекулах как о материальных точках оправдывается только для одноатомных газов. В случае многоатомных газов нужно рассматривать молекулы как сложные системы, способные вращаться как целое, причем атомы в них могут совершать колебания вблизи своих положений равновесия. Общее число степеней свободы молекулы при этом увеличивается. Вспомним, что числом степеней свободы механической системы называется количество независимых параметров, с помощью которых может быть задано положение системы. Так, положение материальной точки в пространстве определяется заданием значений трех ее координат. В соответствии с этим материальная точка имеет три степени свободы. Положение абсолютно твердого тела можно определить, задав три координаты его центра инерции и три угла, характеризующие возможные повороты тела в пространстве. Таким образом, абсолютно твердое тело имеет шесть степеней свободы — три поступательных и три вращательных. N материальных точек, не связанных между собой, имеют 3N степеней свободы. Поскольку положение в пространстве системы как целого точно так же, как и положение абсолютно твердого тела определяется шестью параметрами, упомянутыми выше, то число степеней свободы такой системы равно 3· N -6. Это число соответствует возможным смещениям точек относительно друг друга около своих положений равновесия. Такой тип движения называется колебательным. Значит, количество колебательных степеней свободы и есть 3· N -6. Энергия молекул, состоящих из некоторого числа атомов, не жестко связанных друг с другом, будет теперь складываться из энергии поступательного движения, вращательной энергии и энергии колебаний Ei = Eпоступ + Eвращ + Eколеб. (2.26) Нет причин полагать, что поступательное движение является в какой-то мере выделенным по сравнению с вращательным или колебательным. Поэтому следует считать, что по-прежнему на каждую степень свободы молекулы приходится энергия, равная kT /2. Однако следует учесть особенность, связанную с колебательным движением. Средняя энергия колебательного движения складывается из средней кинетической энергии и равной ей средней потенциальной энергии. Поэтому на каждую колебательную степень свободы приходится энергия, в два раза большая, чем на поступательные или вращательные степени свободы. Следовательно, средняя энергия молекулы должна равняться: < Ei > = i · k · T, (2.27) где i — сумма числа поступательных, вращательных и удвоенного числа колебательных степеней свободы молекулы: i = iпоступ + iвращат + 2· iколеб. (2.28) Внутренняя энергия на один моль идеального газа
Работа идеального газа:
|

 , (2.24)
, (2.24)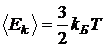 . Эта энергия распределяется между тремя поступательными степенями свободы.
. Эта энергия распределяется между тремя поступательными степенями свободы. .
. . (2.29)
. (2.29)



