Принцип относительности Галилея.
Всякое механическое явление при одних и тех же начальных условиях протекает одинаково в любой инерциальной системе отсчёта. Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой[1]. Термин был предложен Филиппом Франком в 1909 году.[2] Преобразования Галилея опираются на принцип относительности Галилея, который подразумевает одинаковость времени во всех системах отсчета («абсолютное время»[3]). Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.
Вид преобразований при коллинеарных осях Если ИСО S движется относительно ИСО S' с постоянной скоростью
или, используя векторные обозначения,
(последняя формула остается верной для любого направления осей координат). Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).
Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей Формула преобразования скоростей Достаточно продифференцировать
Рассмотрим преобразование произвольного сдвига начала отсчета на вектор где радиус-вектор какого-то тела A в системе отсчета K обозначим за подразумевая, как всегда в классической механике, что время Тогда в любой момент времени
и в частности, учитывая
имеем:
где:
Если
или короче
— как для средних, так и для мгновенных скоростей (формула сложения скоростей). Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга:
|

 вдоль оси
вдоль оси  , а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:
, а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид: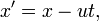

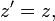




 (много меньше скорости света).
(много меньше скорости света). в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.
в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости. ,
, ,
, в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени:
в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени:  .
.
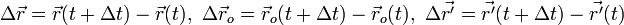 ,
,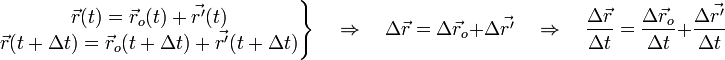

 — средняя скорость тела A относительно системы K;
— средняя скорость тела A относительно системы K;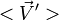 — средняя скорость тела А относительно системы K';
— средняя скорость тела А относительно системы K'; — средняя скорость системы K' относительно системы K.
— средняя скорость системы K' относительно системы K.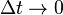 то средние скорости совпадают с мгновенными:
то средние скорости совпадают с мгновенными:





