Средние величины.
Группировка статистических данных и ее роль в анализе информации
Равный интервал, величина интервала - Формула Стерджесса (величина интервала) -
Абсолютные, относительные, средние величины Относительные величины Относительные величины (ОВ) динамики характеризуют изменение явления во времени. (Коэффициент роста) Темп роста – с переменной базой - С постоянной базой - ОВ планового задания - ОВ выполнения плана - ОВ динамики - ОВ структуры характеризуют долю отдельных частей в общем объеме совокупности (удельный вес) - ОВ координации отражают отношение численности двух частей единого целого, т. е. показывают, сколько единиц одной группы приходится в среднем на одну, на 10 или на 100 единиц другой изучаемой совокупности. ОВ координации - ОВ наглядности (сравнения) отражают результаты сопоставления одноименных показателей, относящихся к одному и тому же периоду времени, но к разным объектам или территориям (например, сравнивается годовая производительность труда по 2-м предприятиям) ОВ сравнения -
Средние величины Степенные средние общего типового расчета: Средняя степенная простая - Ср едняя степенная взвешенная -
Гармоническая простая – когда небольшая совокупность и индивидуальные значения не повторяются. Используется, если исчисляем среднюю из обратных величин. Средняя квадратическая – для расчета среднего квадратического отклонения, являющегося показателем вариации признаков Средняя геометрическая простая – для вычисления среднего коэффициента роста (темпа) в рядах динамики, если промежутки, к которым относятся коэффициенты роста, одинаковы.
|


 , m – число групп
, m – число групп , n – число наблюдений
, n – число наблюдений yn – уровень явления за период (например, выпуск продукции по кварталам года)
yn – уровень явления за период (например, выпуск продукции по кварталам года)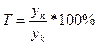 , yk – постоянная база сравнения
, yk – постоянная база сравнения





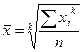 ,
,  - индивидуальное значение признака, по которому рассчитывается средняя, n – объем совокупности (число единиц)
- индивидуальное значение признака, по которому рассчитывается средняя, n – объем совокупности (число единиц) , fi – частота повторения индивидуального признака (
, fi – частота повторения индивидуального признака ( =n)
=n)
 ,
, 



 ,
, 

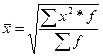
 гарм. <
гарм. < 


