Выборочное наблюдениеN – объем генеральной совокупности n – объем выборочной совокупности (число единиц, попавших в выборку)
р – генеральная доля (доля единиц, обладающих данным признаком в генеральной совокупности) w – выборочная доля
S – среднее квадратическое отклонение признака в выборочной совокупности.
Неравенство Чебышеба При неограниченном числе наблюдений, независящих друг от друга из генеральной совокупности с вероятностью сколь угодно близкой к 1, можно утверждать, что расхождение между выборочной и генеральной средней будет сколь угодно малой величиной
Теорема Ляпунова Дает количественную оценку ошибки. При неограниченном объеме из генеральной совокупности с Р расхождения выборочной и генеральной средней равна интегралу Лапласа
Р – гарантированная вероятность t – коэффициент доверия, зависящий от Р
Средняя ошибка (n>30) при случайной повторной выборке:
При случайной бесповторной выборке:
|
- генеральная средняя (среднее значение признака в генеральной совокупности)
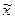- выборочная средняя
- генеральная дисперсия
- выборочная дисперсия
- среднее квадратическое отклонение признака в генеральной совокупности
.
, 
- нормированная функция Лапласа (интеграл Лапласа)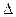
- предельная ошибка выборки
, 
- стандартная среднеквадратическая ошибка
, 
- предельная (максимально возможная) ошибка средней, t – коэффициент кратности средней ошибки выборки, зависящий от вероятности, с которой гарантируется величина предельной ошибки
, 
- предельная (максимально возможная) ошибка доли
, 
, 
