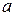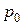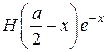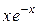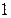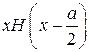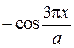Свойства изотропного материала
1. Найти функцию напряжений 2. Построить пространственную зависимость 3. Найти компоненты напряженного состояния в пластине 4. Построить пространственные зависимости 5. Определить граничные условия на контурах 6. Определить главные напряжения 7. Построить линии уровня главных напряжений 8. Построить линии уровня главных касательных напряжений 9. Изобразить в относительном масштабе заданную пластину и соответствующие граничные условия на контурах
Примечание: 1. При проведении расчетов ограничится десятью членами ряда Фурье. 2.
|
Задача №3. Для пластины единичной толщины, находящейся в плоском напряженном состоянии (рис. 1), пользуясь методом тригонометрических рядов
.
.
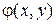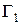и 
.
и 
, соответствующие приложенной нагрузке на контурах 
и 
.
в пластине и простроить пространственные зависимости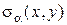 
.
(изобары).
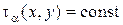(изохромы).
.
- функция Хевисайда.
